Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left\{{}\begin{matrix}S=\dfrac{V}{l}\\S'=\dfrac{V}{2l}\end{matrix}\right.\Leftrightarrow\dfrac{S}{S'}=\dfrac{\dfrac{V}{l}}{\dfrac{V}{2l}}=2\)
\(\left\{{}\begin{matrix}R=p\dfrac{l}{S}\\R'=p\dfrac{2l}{S'}\end{matrix}\right.\Leftrightarrow R'=p\dfrac{4l}{S}=4R\)
\(\Rightarrow R'=4\cdot3=12\Omega\)

Chọn B. Điện trở của dây dẫn giảm đi 10 lần
Áp dụng công thức: 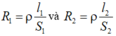
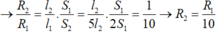

Ta có: \(R=\delta\dfrac{l}{S}\)
Ta thấy rằng tiết diện tỉ lệ nghịch với điện trở dây dẫn nên khi tăng/giảm tiết diện dây đó lên 5 lần thì điện trở sẽ giảm/tăng đi 5 lần.
Điện trở của dây dẫn khi tiết diện tăng là:
\(R_t=\dfrac{R}{5}=2\left(\Omega\right)\)
Điện trở của dây dẫn khi tiết diện giảm là:
\(R_g=5R=50\left(\Omega\right)\)

Ta có công suất hao phí trên đường dây dẫn điện:
\(P_{hp}=\dfrac{P^2\cdot R}{U^2}\)
Nếu tăng \(U^2\) lên 100 lần và giảm \(R\) đi 2 lần thì:
\(P_{hp}'=\dfrac{P^2\cdot\dfrac{R}{2}}{U^2\cdot100}=\dfrac{P_{hp}}{200}\)
Vậy công suất hao phí giảm 200 lần.

\(\dfrac{R_1}{R_2}=\dfrac{\rho\dfrac{l_1}{S_1}}{\rho\dfrac{l_2}{S_2}}=\dfrac{l_1}{S_1}.\dfrac{S_2}{l_2}=\dfrac{l_1}{S_1}.\dfrac{\dfrac{1}{2}S_1}{3l_1}=\dfrac{1}{6}\Rightarrow R_2=6R_1\)
Vậy điện trở của dây tăng gấp 6 lần

\(\Rightarrow\left\{{}\begin{matrix}I=\dfrac{U}{R}\\I'=\dfrac{U}{3R}\\I-I'=0,6A\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}I=3I'\\3I'-I'=0,6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}I=3.0,3=0,9A\\I'=0,3A\end{matrix}\right.\)\(\Rightarrow I=0,9A\)

Điện trở của dây là:
\(R=\rho\dfrac{l}{S}=2,8\cdot10^{-8}\cdot\dfrac{10}{0,1\cdot10^{-6}}=2,8\Omega\)
Tiết diện dây sau khi tăng là:
\(S'=2\cdot0,1\cdot10^{-6}=0,2\cdot10^{-6}\left(m^2\right)\)
\(\Rightarrow R'=\rho\dfrac{l}{S'}=2,8\cdot10^{-8}\cdot\dfrac{10}{0,2\cdot10^{-6}}=1,4\Omega\)

16 lần
cách giải thế nào bạn ơi?