
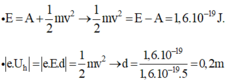
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

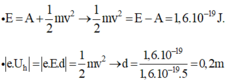

Electron chuyển động đều tức là lực điện cân bằng với lực từ:
\(F_E=F_B\)
\(\Rightarrow eE=evB\)
\(\Rightarrow v=\frac{E}{B}=10^6\left(\text{m/s}\right)\)
Động năng của electron:
\(T=\frac{m_ev^2}{2}\)
Năng lượng của photon cung cấp công thoát cho electron và cho electron vận tốc đầu (động năng):
\(h\frac{c}{\lambda}\text{=}E_{th}+T\) (\(E_{th}\)là công thoát)
\(\lambda=\frac{hc}{E_{th}+T}=1,7.10^{-7}\left(m\right)=0,17\left(nm\right)\)
\(chọn.A\)

Đáp án : C
Áp dụng hệ thức Anhxtanh ta có:
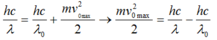
Khi electron chuyển động trong điện trường có cường độ điện trường E thì nó chịu tác dụng của lực điện trường F =|e|.E, công do lực điện trường này cản electron là Ac = F.s, với s là quãng đường mà electron đi được.
Quãng đường tối đa mà electron có thể đi được đến khi dừng lại (v = 0) được tính theo định lý động năng:
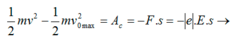
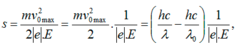
(do v = 0)
Thay số ta tính được s = 0,015 (m) = 1,5 (cm).

Mình hướng dẫn thế này rồi bạn làm tiếp nhé.
a. Áp dụng CT: \(hf=A_t+\dfrac{1}{2}mv^2\)
\(\Rightarrow 6,625.10^{-34}.3.10^8=A_t+\dfrac{1}{2}.9,1.10^{-31}.(0,4.10^6)^2\)
\(\Rightarrow A_t\)
Mà \(A_t=\dfrac{hc}{\lambda_0}\Rightarrow \lambda_0\)
b. Áp dụng: \(\dfrac{hc}{\lambda}=A_t+eV_{max}\)
\(\Rightarrow \lambda\)