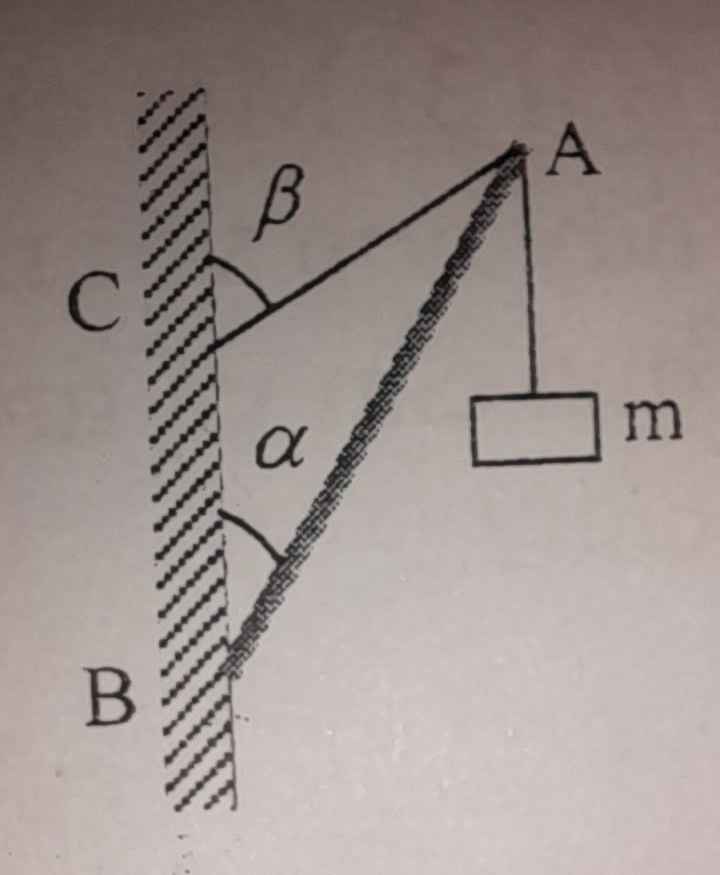
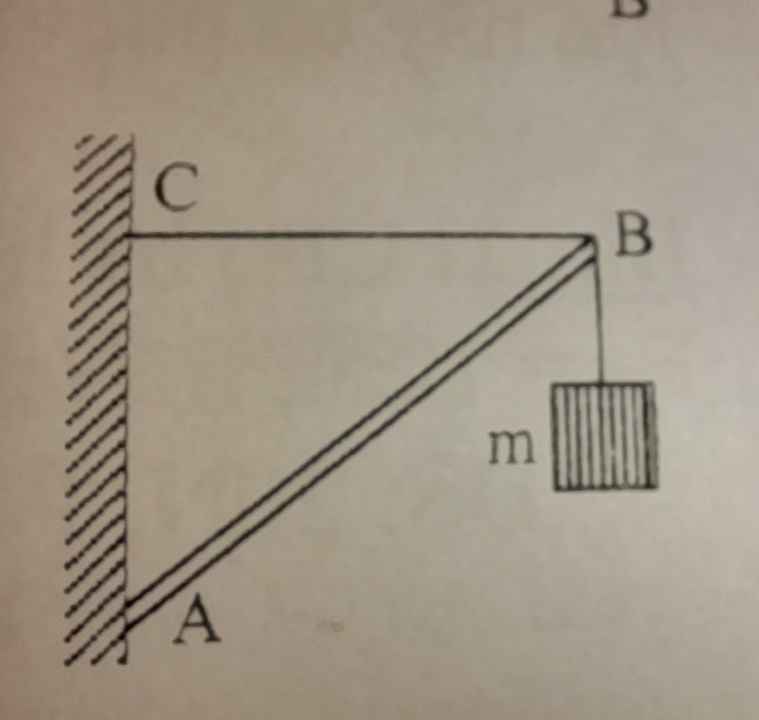
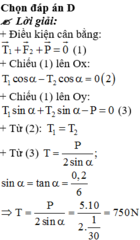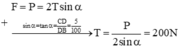Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

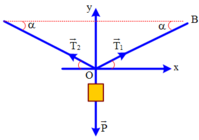
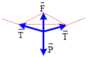
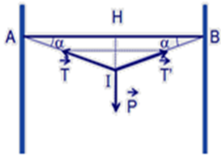
Vẽ hình, phân tích lực ta được:
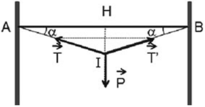
Theo đề bài, ta có:
T=T′
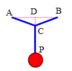
IH=0,5m;HA=4m
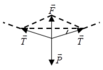
+ Vật cân bằng: P → + T → + T ' → = 0 →
Từ hình ta có: P=2Tsinα
Mặt khác, ta có:
tan α = I H H A = 0 , 5 4 = 1 8 → s i n α = 0 , 124 → T = P 2 s i n α = m g 2 s i n α = 6.10 2.0 , 124 = 241 , 9 ( N )
Đáp án: B

Chọn trục quay đi qua đầu B (quy ước chiều dương cùng chiều với đồng hồ quay)
Vì hệ đang cân bằng nên ta có: \(\sum M=0\)
\(\Leftrightarrow F.AB-P_m.CB=0\)
\(\Leftrightarrow10.100-10m.20=0\)
\(\Leftrightarrow m=5\left(kg\right)\)
Áp dụng định luật II Newton vào thanh AB có:
\(\overrightarrow{F}+\overrightarrow{P_m}+\overrightarrow{T_B}=\overrightarrow{0}\)
\(\Rightarrow F-10m+T_B=0\)
\(\Leftrightarrow T_B=10.5-10=40\left(N\right)\)

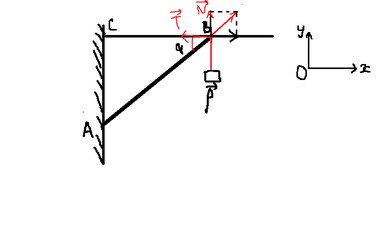
Các lực tác dụng lên thanh AB.
+Trọng lực \(\overrightarrow{P}\) hướng xuống.
+Lực căng dây \(\overrightarrow{T}\).
+Phản lực \(\overrightarrow{N}\).
Tổng hợp lực: \(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{T}=\overrightarrow{0}\left(1\right)\)
Chiếu (1) lên trục \(Oxy\) ta đc:
\(Ox:N\cdot cos\alpha-T=0\Rightarrow T=N\cdot cos\alpha\)
\(Oy:N\cdot sin\alpha-P=0\Rightarrow P=N\cdot sin\alpha\)
\(cos\alpha=\dfrac{BC}{AB}=\dfrac{0,6}{1}=0,6\)
\(\Rightarrow sin\alpha=\sqrt{1-cos^2\alpha}=\sqrt{1-0,6^2}=0,8\)
\(\Rightarrow N=\dfrac{P}{sin\alpha}=\dfrac{10m}{sin\alpha}=\dfrac{10\cdot1}{0,8}=12,5N\)
Lực căng dây:
\(T=N\cdot cos\alpha=12,5\cdot0,6=7,5N\)