Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi chiều cao của tòa tháp là h \(\left(m,h>0\right)\)
Chiều cao của tòa tháp là:
\(\frac{13,1}{0,1}=\frac{h}{2}\Rightarrow h=\frac{13,1\times2}{0,1}=262\left(m\right)\)(TM)
Vậy chiều cao của toà tháp là \(262m\)

P/s:mình vẽ hình rồi đặt tên luôn cho tam giác.
Xét ΔABC và ΔMNP ta có
\(\widehat{ABC}=\widehat{MNP}=90^0\)
Vì toà nhà được chiếu ánh sáng cùng thời điểm \(\rightarrow\widehat{ACB}=\widehat{MPN}\)
⇒ ΔABC ∼ ΔMNP(gg )
⇒\(\dfrac{AB}{MN}=\dfrac{BC}{NP}hay\dfrac{AB}{3}=\dfrac{23}{65}\)
\(\Rightarrow AB=\dfrac{3.23}{6,5}=10,6\)(m)
Vậy toà nhà cao 10,6m
:v đề sai hay cậu sai đây nhỉ mà là 65 mà ta
với lại mình chưa hiểu lắm chỗ này á...
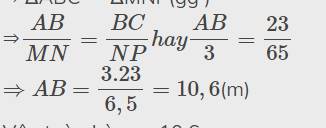
tỉ lệ thì đúng rồi mà lúc thay số vào lại là lạ à nhen:))
nếu cậu làm: \(\dfrac{AB}{MN}=\dfrac{BC}{NP}\)
ý cậu là AB là độ cao của toàn nhà, BC là bóng của toàn nhà;
MN là chiều cao cột sắt, NP là bóng của cột sắt (à mấy bài này cậu phải nêu cái này ra á không là trừ 0.25 điểm;))
như vậy thì AB=?, BC= 23 m, MN= 65m, NP= 3m nè thay vào thì được kết quả rất là lớn
Nên mình nghĩ là đề sai đó, mà làm sao mà 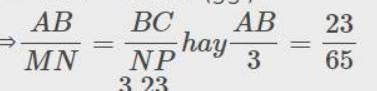
hai cái này nó tương đương được ha cậu, hay là mình chưa xem kĩ nhỉ?
MN đang là 65 thì thành 3, NP đang là 3 thì thành 65 cái này là cách biến đổi mới hả cậu ơi:(
mà mình thấy cậu làm bài nó hơi kì nhé:

Ủa vậy là 65 hay 6.5. Mình thấy số 6.5 cũng hợp lí mà dựa vào đâu cậu biết đó là số 6.5 mà tính đây? Hay thật đó!
Vậy là đề sai hay cậu sai nhỉ?

ΔABM đồng dạng với ΔCDM'
=>AB/CD=AM/CM'
=>AB=3*184,5/32=17,3(m)

a: Xét ΔABC có DE//BC
nên AN/AB=AM/AC
=>1,5/AB=2,4/5,3
=>\(AB\simeq3,3125\left(m\right)\)
b: 
Xét ΔABC có DE//BC
nên DE/BC=AE/AC=(AC-CE)/AC
=>36-x=1,6*36/24=2.4
=>x=33,6(m)
a) Xét tam giác \(ABC\) có \(MN//BC\) nên theo định lí Thales ta có:
\(\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}} \Leftrightarrow \frac{{1,5}}{{AB}} = \frac{{2,4}}{{2,4 + 2,9}} \Rightarrow AB = \frac{{1,5.\left( {2,4 + 2,9} \right)}}{{2,4}} = 3,3125\)
Vậy chiều cao \(AB\)của cái cây là 3,3125m.
b) Đặt tên các điểm như hình vẽ

Xét tam giác \(ABC\) có \(DE//BC\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{DE}}{{BC}} = \frac{{AE}}{{AC}} = \frac{{AC - CE}}{{AC}} \Leftrightarrow \frac{{1,6}}{{24}} = \frac{{36 - x}}{{36}}\)
\( \Rightarrow 36 - x = \frac{{1,6.36}}{{24}} \Leftrightarrow x = 36 - \frac{{1,6.36}}{{24}} = 33,6\)
Vậy người đó có thể đứng xa tòa nhà nhất là 33,6m.

tòa nhà bóng thanh sắt bóng 57,625 1,6 0,2 A B C N M P mặt trời
Mặt trời chiếu các tia song song dẫn đến
AC//MP (1)
mặt khác tòa nhà và thanh sắt cùng vuông góc với mặt đất nên song song với nhau
=> AB//MN (2)
Từ (1) , (2)
=> \(\widehat{BAC}=\widehat{NMP}\)
=> Hai tam giác vuông BAC và NMP đồng dạng
=> \(\frac{BA}{MN}=\frac{BC}{NP}\)=> \(AB=\frac{MN.BC}{NP}=57,625.\frac{1,6}{0,2}=461\)
Vậy chiều cao tòa nhà là 461m

