Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Mỗi lần di chuyển, quân cờ chỉ có thể di chuyển một trong bốn cách sau: lên trên 1 ô (U), xuống dưới 1 ô (D), sang phải 1 ô (R), sang trái 1 ô (L). Quân cờ di chuyển bốn lần sẽ có 4 4 = 256 cách.
⇒ n ( Ω ) = 256 cách
Gọi A là biến cố quân cờ không trở về đúng vị trí ban đầu sau bốn lần di chuyển.
=> A ¯ là biến cố quân cờ trở về đúng vị trí ban đầu sau bốn lần đi chuyển.
Để quân cờ trở về đúng vị trí ban đầu sau bốn lần đi chuyển thì phải thực hiện 1 trong 3 trường hợp sau:
Trường hợp 1: Có một U, một D, một R, một L.
Xếp cách thực hiện U, D, R, L theo thứ tự có 4! = 24 cách.
Trường hợp 2: Có hai U, hai D.
Xếp cách thực hiện hai U, hai D theo thứ tự có ![]() cách.
cách.
Trường hợp 3: Có hai R, hai L.
Xếp cách thực hiện hai R, hai L theo thứ tự có ![]() cách.
cách.
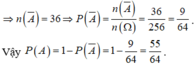

2, sin4x+cos5=0 <=> cos5x=cos\(\left(\frac{\pi}{2}+4x\right)\Leftrightarrow\orbr{\begin{cases}x=\frac{\pi}{2}+k2\pi\\x=-\frac{\pi}{18}+\frac{k2\pi}{9}\end{cases}\left(k\inℤ\right)}\)
ta có \(2\pi>0\Leftrightarrow k< >\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(\frac{\pi}{2}\)khi k=0
\(-\frac{\pi}{18}+\frac{k2\pi}{9}>0\Leftrightarrow k>\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(-\frac{\pi}{18}-\frac{k2\pi}{9}\)là \(\frac{\pi}{6}\)khi k=1
vậy nghiệm dương nhỏ nhất của phương trình là \(\frac{\pi}{6}\)
\(\frac{\pi}{2}+k2\pi< 0\Leftrightarrow k< -\frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(\frac{\pi}{2}+k2\pi\)là \(-\frac{3\pi}{2}\)khi k=-1
\(-\frac{\pi}{18}+\frac{k2\pi}{9}< 0\Leftrightarrow k< \frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(-\frac{\pi}{18}+\frac{k2\pi}{9}\)là \(-\frac{\pi}{18}\)khi k=0
vậy nghiệm âm lớn nhất của phương trình là \(-\frac{\pi}{18}\)

Đáp án A
Để nhân vật game trở về vị trí ban đầu thì số lần nhất nút di chuyển lên bằng số lần nhấn nhút di chuyển xuống và số lần nhấn nút di chuyển sang trái bằng số lần nhấn nút di chuyển sang phải.
Số cách nhấn nút cho 4 lần di chuyển là 44 cách.Vậy
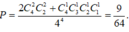

Trả lời:
a) Vận tốc của chuyển động khi t = 2 (s).
Ta có:
v=dsdt=S′=3t2−6t−9v=dsdt=S′=3t2−6t−9
Khi t = 2(s) ⇒ 3.22 – 6.22 – 9 = -9 m/s.
b) Gia tốc của chuyển động khi t = 3(s). Ta có:
a=dvdt=v′=6t−6a=dvdt=v′=6t−6
Ở t = 3(s) ⇒ a = 6.3 – 6 = 12 m/s2
c) Ta có: v = 3t2 – 6t – 9
Tại thời điểm vận tốc triệt tiêu:
v=0⇔3t2−6t−9=0⇔t2−2t−3=0⇔[t=−1(l)t=3(s)v=0⇔3t2−6t−9=0⇔t2−2t−3=0⇔[t=−1(l)t=3(s)
Gia tốc: a = 6t – 6.
Khi t = 3s ⇒ a = 6.3 – 6 = 12 m/s2
d) Ta đã có a = 6t – 6.
Khi a = 0 ⇔ 6t – 6= 0 ⇔ t = 1(s)
Lại có: v = 3t2 – 6t – 9
Khi t = 1(s) ⇒ v = 3.12 – 6.1 – 9 = -12 m/s
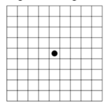
Phương pháp: Chia đường đi của thỏ thành 2 giai đoạn, tính số phần tử của không gian mẫu và số phần tử của biến cố A « thỏ đến được vị trí B » .
Cách giải :
Từ A đến B nhất định phải đi qua D, ta chia làm 2 giai đoạn A → D và D → B
Từ A → D có 9 cách.
Từ D → B có 6 cách tính cả đi qua C và có 3 cách không đi qua C.
Không gian mẫu n Ω = 9 . 6 = 54
Gọi A là biến cố « thỏ đến được vị trí B » thì nA = 9.3 = 27
Vậy