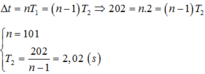Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Sau khoảng thời gian Δt, con lắc 1 thực hiện được n1 dao động và con lắc 2 thực hiện được n2 dao động:
Δ t = n 1 T 1 = n 2 T 2 ⇒ n 1 n 2 = T 2 T 1 = 0 , 85 1 , 13 = 85 113 ⇒ n 1 = 85 n n 2 = 113 n
⇒ Δ t = 85 n T 1 = 96 , 05 n s ⇒ Δ t min = 96 , 05 s
Chọn đáp án B

Đáp án C
Phương pháp: Sử dụng lí thuyết về bài toán con lắc đơn chịu thêm tác dụng của lực điện trường
Công thức xác định chu kì dao động của con lắc lò xo và con lắc đơn:
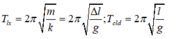
Cách giải:
- Chu kì dao động của con lắc lò xo:
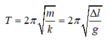
Khi đặt trong điện trường thì không làm thay đổi khối lượng và độ cứng của lò xo nên chu kì dao động của lò xo khi không có điện trường và có điện trường:
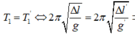
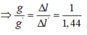
- Chu kì dao động của con lắc đơn khi không có điện trường và có điện trường là:
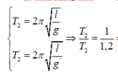
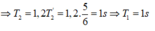

\(T=2\pi\sqrt{\frac{l}{g}}\)
\(T'=2\pi\sqrt{\frac{l'}{g}}\)
\(\Rightarrow\frac{T'}{T}=\sqrt{\frac{l'}{l}}=\sqrt{2}\Rightarrow T'=2\sqrt{2}s\)

Đáp án A
Cần lưu ý: Chu kì của con lắc lo xo (CLLX)
chỉ phụ thuộc vào độ cứng k và khối lượng m.
Do đó khi đặt vào trong điện trường đều thì chu kì CLLX không thay đổi. Chu kì của con lắc đơn phụ thuộc vào gia tốc trọng trường nơi treo con lắc.
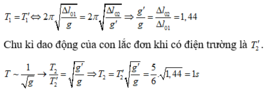

\(\overrightarrow {g'} =\overrightarrow g - \overrightarrow a \)
Ô tô chuyển động nằm ngang => \(\overrightarrow a \bot \overrightarrow g\)
=> \(g' = \sqrt{g^2+ a^2}\)
\(T = 2\pi \sqrt{\frac{l}{g}}\)
\(T' = 2\pi \sqrt{\frac{l}{g'}}\)
=> \(\frac{T}{T'} = \sqrt{\frac{g'}{g}} = \sqrt{\frac{\sqrt{g^2+a^2}}{g}} = 1,01\)
=> \(T'= \frac{2}{1,01} = 1,98 s.\)
cho mình hỏi: Nếu trong trường hợp ôtô chuyển động thẳng chậm dần đều thì phải làm ntn ?

Đáp án A
Khi có điện trường thì vị trí cân bằng mới của 2 lò xo cách nhau 2A.
+ Chọn gốc tọa độ trùng với O1 ta có:
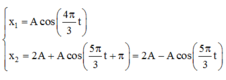
Hai con lắc có cùng chiều dài khi cả 2 cùng về vị trí cân bằng ban đầu.
+ Khoảng thời gian chúng có cùng chiều dài từ thời điểm ban đầu là Dt = n1T1 = n2T2

* Dt = 4nT1 = 6n
* Lần thứ 3 nên Dt = 18 s
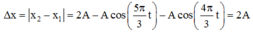
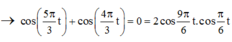

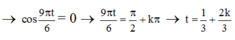
+ Với 0 < t £ 18 => -0,5 < k ≤ 26,5
=> k = 0, …, 26 => Có 27 giá trị của k