Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Delta l=\frac{g}{\omega^2}=0,25m\)
\(t=0\Rightarrow x=5\sqrt{3}cm\Rightarrow l=l_0+\Delta l+x=158,66cm\)
Vậy không phương án đúng

Ban đầu t = 0 thì x = 2 cm, lúc này vật đang ở biên độ dương.
Quả cầu dao động được nửa chu kì thì x = -2 cm (vật ở biên độ âm)
Chiều dài của lò xo: \(\ell=\ell_0+\Delta\ell_0+x=40+10-2=48(cm)\)

\(x=2\sin(\omega t +\dfrac{\pi}{2})=2\cos(\omega t)\) (cm)
Như vậy, ban đầu (t = 0) vật đang ở biên độ dương \(x=2cm\)
Khi quả cầu đi được nửa chu kì dao động thì nó sẽ lên biên độ âm, \(x=-2cm\)
Chiều dài lò xo: \(\ell=\ell_0+\Delta \ell_0+x=40+10-2=48(cm)\)

Chọn D

+ T = 1s => ω = 2π rad/s.
+ Độ biến dạng của lò xo ở vị trí cân bằng:
![]()
+ Biên độ dao động:
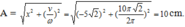
+ Thời điểm t = 0 tương ứng với một gốc lùi Δφ = ωt = 2π.2,5 = 5π trên đường tròn.
+ Lực đàn hồi khi đó có độ lớn:
Fđh = k(Δlo + x) = k(25 + 5√2). 10-2 N.
Kết hợp với Fđhmin = k.(Δlo - A) = k. 15.10-2 = 6N.
+ Từ hai biểu thức trên ta thu được Fđh = 12,82N.

Chọn đáp án D
A = l max − l min 2 = 56 − 40 2 = 8 ( c m ) ; ω = 2 π f = 10 π t
l C B = 56 − 8 = 48 ( c m )
Tại t = 0 ⇒ x = − 4 v < 0 ⇒ cos ϕ = − 1 2 sin ϕ > 0 ⇒ ϕ = 2 π 3
Vậy: x = 8 cos 10 π t + 2 π 3

\(\Delta l=5cm\)
Vị trí có lực đẩy đàn hồi lần thứ nhất chính là vị trí lò xo bắt đầu bị nén. Tức là qua vị trí -\(x=-\Delta l\).
M -10 10 N -5 ^
Vị trí ban đầu t = 0 tại M ứng với góc (-90 độ).
Vị trí lực đầy đàn hồi lần thứ nhất tại N x = -5 cm.
=> \(\varphi=\pi+\frac{\pi}{6}=\frac{7\pi}{6}\Rightarrow t=\frac{\varphi}{\omega}=\frac{7\pi}{6.10\pi}=\frac{7}{60}s.\)
sai rồi bạn ơi, lực đẩy max là lúc vật ở vị trí -A nhé, denta phi sẽ là 3π/2, và t sẽ là 3/20s

Hướng dẫn:
+ Tần số góc của dao động ω = k m = 10 π rad/s.
Độ biến dạng của lò xo tại vị trí cân bằng Δ l 0 = m g k = 1 c m
+ Khi vật đang ở vị trí có li độ x = –1 cm → l = l 0 = 40 c m , người ta tiến hành giữ cố định lò xo tại điểm cách điểm cố định 20 cm → lò xo mới tham gia vào dao động có độ cứng k' = 2k = 200 N/m.
+ Năng lượng của con lắc trước khi cố định lò xo: E t = k x 2 = 0 , 01 E d = 1 2 k A 2 − x 2 = 0 , 035 J
→ Năng lượng của hệ sau cố định lò xo đúng bằng tổng động năng và một nửa thế năng của vật trước khi cố định lò xo.
E ' = 0 , 5 k A ' 2 = E d + 0 , 5 E t = 0 , 04 J → A' = 0,02 cm.
→ Lực đàn hồi cực đại F m a x = k ' ( 0 , 5 Δ l 0 + A ' ) = 6 N .
Đáp án B

Đáp án A
+ Độ giãn của lò xo tại vị trí cân bằng Δ l 0 = m g k = 0 , 1.10 100 = 1 cm.
Tần số góc dao động của con lắc ω = k m = 10 10 rad/s.
+ Vận tốc truyền cho vật m so với điểm treo có độ lớn v 0 = 10 + 40 = 50 cm/s.
→ Biên độ dao động của vật sau đó A = v 0 ω = 50 10 10 = 1 , 58 cm.
→ Chiều dài cực đại l m a x = l 0 + Δ l 0 + A = 27 , 58 c m .

tại thời điểm t=0, x=4.cos(\(ω-π/2 \))=4.cos(-\(π/2\))=0(cm)
ta có:
Fđ max=k(\(∆lo+A\))
Fđmin=k(\(∆lo-A\))
\(\frac{Fđmax}{Fđmin}= \frac{5}{3} <=> \frac{k(\Delta lo +A)}{k(\Delta lo -A)}=\frac{5}{3}<=>\frac{\Delta lo +A}{\Delta lo -A}=\frac{5}{3}\)
mà A=4cm =>\(\Delta lo \)=16cm
=>chiều dài của lò xo tại thời điểm t=0 là l'=lo+\(\Delta lo \)+x=48+16+0=64cm