Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(f=\frac{1}{2\pi}\sqrt{\frac{g}{\Delta l}}=\frac{1}{2\pi}\sqrt{\frac{\pi^2}{0.16}}=1.25Hz\)

k=100N/m
x=0,03m
v=2\(\pi.10^{-2}m\)/s
W=0,5=\(\frac{1}{2}\)m\(\omega^2.A^2\) \(\Rightarrow\)m=\(\frac{1}{\omega^2A^2}\)
Dùng công thức độc lập:
\(\frac{x^2}{A^2}+\frac{v^2}{\omega^2A^2}=1\\ \Leftrightarrow x^2m\omega^2+v^2.m=1\\ \Leftrightarrow x^2.k+v^2.m=1\)
\(\Rightarrow m\)
Có m thay vào \(\omega=\sqrt{\frac{k}{m}}\)
Có \(\omega\Rightarrow T\)

Đáp án B
+ Độ biến dạng của lò xo tại vị trí cân bằng
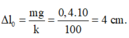
+ Đưa vật đến vị trí lò xo không biến dạng rồi thả nhẹ
![]()
+ Động năng của vật bằng thế năng lần đầu tiên tại vị trí
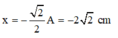
(trục Ox thẳng đứng, hướng xuống).
Lực đàn hồi có độ lớn
![]()

Vẽ vòng tròn ta ta có thể thấy được vị trí góc pha mà thế năng bằng động năng là
\(\varphi=\left(2k+1\right)\frac{\pi}{4}\)
Cứ sau góc \(\frac{\pi}{2}\) thì thế năng bằng động năng tương ứng với T/4
hu kỳ dao động là T = 0.2s suy ra \(\omega=10\pi\)
\(k=\omega^2m=\frac{50N}{m}\)

Độ biến dạng của lò xo khi vật ở VTCB là: \(\Delta \ell_0=\dfrac{mg}{k}=\dfrac{1.10}{100}=0,1m=10cm\)
\(\omega=\sqrt{\dfrac{k}{m}}=10(rad/s)\)
Áp dụng CT: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow A^2=2^2+\dfrac{(20\sqrt 3)^2}{10^2}\)
\(\Rightarrow A = 4cm\)
Lực đàn hồi cực đại:
\(F_{dhmax}=k\Delta\ell_{max}=k(\Delta\ell_0+A)=100.(0,1+0,04)=14(N)\)
Lực đàn hồi cực tiểu:
\(F_{dhmin}=k\Delta\ell_{min}=k(\Delta\ell_0-A)=100.(0,1-0,04)=6(N)\)

Giả sử: \(\pi^2\approx10\)
a) Khối lượng của vật: \(m=\dfrac{k}{\omega^2}=\dfrac{50}{\left(5\pi\right)^2}=0,2kg=200g\)
Chu kì của con lắc: \(T=\dfrac{2\pi}{\omega}=\dfrac{2}{5}\left(s\right)\)
b)Thế năng: \(W_t=\dfrac{1}{2}kx^2=\dfrac{1}{2}\cdot50\cdot0,02^2=0,01J\)
Tại li độ \(x=2cm\) thì \(v=-\omega Asin\left(\pi t+\varphi\right)=-50\pi sin\left(5\pi t+\dfrac{\pi}{2}\right)\Rightarrow t\)
Động năng: \(W_đ=\dfrac{1}{2}mv^2\)
Cơ năng con lắc: \(W=W_đ+W_t=0,24J\)
a) \(k=m\omega^2=50\Rightarrow m=0,2\left(kg\right)\)
\(T=\dfrac{2\pi}{\omega}=0,4\left(s\right)\)
b) \(W_t=\dfrac{1}{2}kx^2=0,01\left(J\right)\)
\(W=\dfrac{1}{2}kA^2=0,25\left(J\right)\)
\(W_đ=W-W_t=0,24\left(J\right)\)
c) \(\Delta l=\dfrac{mg}{k}=0,04\left(m\right)\)
\(v=\dfrac{1}{2}v_{max}\Rightarrow x=\dfrac{A\sqrt{3}}{2}=5\sqrt{3}\left(cm\right)=0,05\sqrt{3}\left(m\right)\)
\(F_{đh}=k\left(\Delta l+x\right)\approx6,33\left(N\right)\)