

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Giải thích: Đáp án B
Phương pháp: áp dụng công thức tính lực phục hồi của con lắc lò xo F =- kx và công thức tính lực đàn hồi
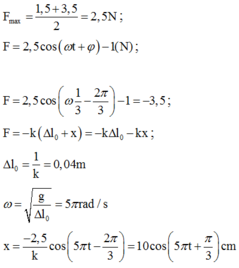

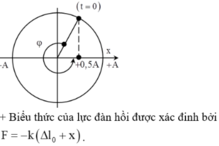
Từ hình vẽ với 2 vị trí cực đại và cực tiểu của lực đàn hồi ta có
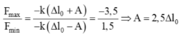
Tại t=0 và thời điểm lực đàn hồi cực đại ta có


Giải thích: Đáp án C
Từ đồ thị ta có hệ:
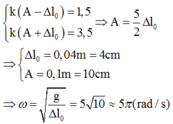
Biểu thức của lực đàn hồi có dạng: ![]()
Lúc t = 0, 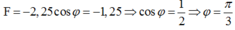

Tại VTCB : đental = 2.5cm
biên độ : A=(30 - 20)/2 = 5cm
vậy thời gian cần tính là t = T/4 + T/12
0k???
Bài 2 hỏi độ lớn của vật là cái j hả??????
Bai 3. oomega = 20rad/s
tại VTCB denta l = g/omega^2 = 2,5cm
A = 25 - 20 - 2,5 = 2,5cm
li độ tại vị trí lò xo có chiều dài 24cm x=24-22,5 = 1,5cm
Áp dụng CT độc lập với thời gian ta tính được v = 40cm/s
từ đó suy ra động năng thui

\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

\(T=2\pi\sqrt{\frac{\Delta l_0}{9}}=0,4s\)
\(\Rightarrow\Delta l_0=4=\frac{A\sqrt{2}}{2}\)
Thời gian lò xo không giãn là \(t=2t-\frac{A\sqrt{2}}{2}\Rightarrow-A=\frac{T}{4}=0,10\left(s\right)\)
Vậy D đúng

Chọn A
Từ đồ thị ta thấy T = 0,4 s → ω = 5π rad/s.
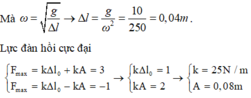
Từ t = 0 đến t = 0,1 s (trong khoảng thời gian T/4) lực đàn hồi tăng đến giá trị cực đại → φ 0 = π 2 rad.
→ Phương trình li độ x = 8cos(5πt + π/2) cm.

Đáp án D
Từ đồ thị ta thấy T = 0,4 s → ω = 5π rad/s.
Mà
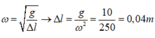
Lực đàn hồi cực đại
Từ t = 0 đến t = 0,1 s (trong khoảng thời gian T/4) lực đàn hồi tăng đến giá trị cực đại
→ 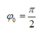 rad.
rad.
→ Phương trình li độ x = 8cos(5πt + π/2) cm