Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp: Sử dụng lí thuyết về dao động điều hòa của con lắc lò xo treo thẳng đứng
Cách giải:
+ Kéo vật xuống dưới đến VT lò xo giãn 6 cm rồi buông không vận tốc đầu => l0 + A = 6 cm = 0,06 m (1)
+ Cơ năng dao động của vật
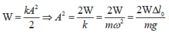

Từ (1) và (2) ta có :
![]()
=> Chọn đáp án A

Chọn đáp án A
Tân số dao đông của con lắc lò xo: f = 1 2 π k m không phụ thuộc vào cách treo và biên độ. Do vậy với m và k không đổi, tần số của con lắc không đổi

Khi vật ở VTCB ta có:
∆l=(mg)/k=g/ω²=10/ω²
=> ω²= 10/∆l (1)
Năng lượng của con lắc:
W = 1/2 m.ω².A² = 0,05
=>ω²A²=0,1 (2)
Thay (1) vào (2) ta được:
A²/∆l =0,01
=>∆l = A²/0,01 = 100A²
Kéo lò xo giãn một đoạn 6 cm
=>∆l + A =0,06
=>100A² +A - 0,06 =0
=>A=0,02 m =2cm
Khi vật ở VTCB ta có: ∆l=(mg)/k=g/ω²=10/ω² => ω²= 10/∆l (1) Năng lượng của con lắc: Nhi Nguyễn (https://hoc24.vn/id/42891) 06/08/2016 lúc 19:10 1 câu trả lời (/hoi-dap/question/72038.html) Được cập nhật Hôm qua lúc 22:24 Vật lý lớp 12 (https://hoc24.vn/vat-ly/hoi-dap/?lop=12) Dao động cơ học (https://hoc24.vn/hoi-dap/dao-dong-co-hoc.4/ ) Một con lắc lò xo treo thẳng đứng, vật có khối lượng m=1kg. Từ vị trí cân bằng kéo vật xuống dưới sao cho lò xo dãn một đoạn 6cm, rồi buông ra cho vật dao động điều hòa với năng lượng dao động là 0,05J. Lấy g=10m/s .Biên độ dao động của vật là bao nhiêu? (/hoi-dap/question/72038.html) 2 T(hrầttnp:H//ohàoncg24S.ơvnn/vip/hoangson) 514 người theo dõi Trường THPT Chuyên Đại học Sư Phạm (http://hoc24.vn/school/34666.truongthpt-chuyen-dai-hoc-su-pham.html) 6 867 303GP 1576SP Theo dõi Gửi tin nhắn 30/8/2017 Hỏi đáp môn Vật lý | Học trực tuyến https://hoc24.vn/vat-ly/hoi-dap/ 4/14 W = 1/2 m.ω².A² = 0,05 =>ω²A²=0,1 (2) Thay (1) vào (2) ta được: A²/∆l =0,01 =>∆l = A²/0,01 = 100A² Kéo lò xo giãn một đoạn 6 cm =>∆l + A =0,06 =>100A² +A - 0,06 =0 =>A=0,02 m =2cm Đúng 1 Bình luận

Chọn đáp án B
Δ l 0 = m g k = 0 , 4.10 100 = 0 , 04 m = 4 c m
⇒ A = Δ l − Δ l 0 = 5 − 4 = 1 c m .

Độ biến dạng của lò xo khi vật ở VTCB là:
\(\Delta l_0=\dfrac{g}{\omega^2}=\dfrac{10}{20^2}=0,025m=2,5cm\)
Theo giả thiết, biên độ: \(A= 5cm.\)
Chọn trục toạ độ có chiều dương hướng xuống. Khi vật qua vị trí lò xo không biến dạng thì \(x=-\Delta l_0 = -2,5cm\)
Áp dụng: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow 5^2=2,5^2+\dfrac{v^2}{20^2}\)
\(\Rightarrow v=50\sqrt 3 (cm/s)=0,5/\sqrt 3 (m/s)\)
Chọn D.

ta có thể sử dụng công thức sau:
E = (1/2)kA^2
Trong đó:
E là cơ năng của vật.k là hằng số đàn hồi của lò xo.A là biên độ dao động.Theo đề bài, cơ năng của vật là 25 mJ = 0.025 J. Với A = 1 cm = 0.01 m, ta có:
0.025 = (1/2)k(0.01)^2
Từ đó, ta có thể tính được hằng số đàn hồi k của lò xo.
Sau khi tính được k, ta có thể tính tần số góc và biên độ dao động của vật bằng công thức:
ω = √(k/m)
A = Amax = (E/k)^(1/2)
Với m = 400 g = 0.4 kg, ta có thể tính được tần số góc và biên độ dao động của vật.