Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Con lắc lò xo nằm ngang → Khi lò xo dãn 2 cm, li độ vật có độ lớn x = 2 c m
→ v = ω A 2 - x 2 = 20 π 3 cm / s . Chọn C.

Chọn đáp án A.
ω = k m = 100 0 , 1 = 10 10 ( r a d / s ) .
Mà A = 2 (cm) => v 0 = ω . A = 10 2 c m / s .
a 0 = ω 2 . A = 1000 2 c m / s 2
v v 0 2 + a a 0 2 = 1 ⇒ 10 10 10 20 2 + a 1000 2 2 = 1
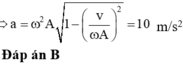
⇒ a = 1000 ( c m / s 2 ) = 10 m / s 2 .

Tần số góc: \(\omega=\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{100}{0,1}}=10\pi(rad/s)\)
Biểu diễn dao động bằng véc tơ quay, tại thời điểm 7/60s thì véc tơ quay đã quay 1 góc là: \(\alpha=\omega.t=\dfrac{7}{6}\pi\)
Tại vị trí \(W_đ=3.W_t\)\(\Rightarrow W=W_đ+W_t=4W_t\)
\(\Rightarrow x=\pm\dfrac{A}{2}=\pm 2cm\)
x 4 -4 2 -2 M N O
Vì tốc độ của vật đang giảm nên có 2 trường hợp:
+ TH1: Dao động ứng với trạng thái tại M, sau khi quay \(\dfrac{7}{6}\pi\) sẽ đến biên âm --> Li độ là -4cm.
+ TH2: Dao động ứng với trạng thái N, sau khi quay \(\dfrac{7}{6}\pi\) sẽ đến biên độ dương -> Li độ là 4cm.

Đáp án B
Phương pháp: Sử dụng đường tròn lượng giác
Cách giải:
Ở vị trí cân bằng là xo bị giãn một đoạn là :
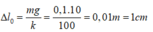
Tần số góc:
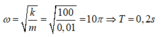
Khi vật dãn 4cm thì vật có li độ x = 3cm nếu chọn chiều dương hướng xuống
Khi x = 3cm thì v = -40 π cm/s ta áp dụng công thức:
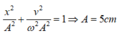
Khi vật bị nén 1,5cm thì lúc đó x = -2,5cm.
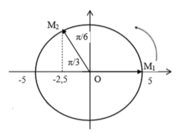
Ta tìm khoảng thời gian ngắn nhất vật đi từ vị trí thấp nhất ( x = A) đến vị trí x = -2,5cm là:
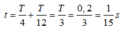
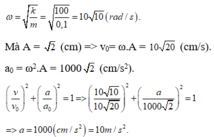



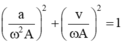
Chọn trục tọa độ có gốc ở vị trí cân bằng.
Con lắc lò xo nằm ngang thì khi lò xo dãn 2cm $\Rightarrow x = 2cm$
Tần số góc \(\omega = \sqrt{\dfrac{k}{m}}= \sqrt{\dfrac{100}{0,1}}=10\pi(rad/s)\)
Áp dụng công thức: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow v = \pm\omega\sqrt{A^2-x^2}= \pm10\pi\sqrt{4^2-2^2}=\pm20\pi\sqrt{3}(cm/s)\)
Chọn trục toạ độ có gốc ở vị trí cân bằng .
Chọn con lò xo nằm ngang thì khi lò xo dãn 2cm.
Ta có công thức:\(A^2=x^2+\dfrac{\upsilon^2}{\omega^2}\)
Tầng số góc \(\omega\) là: \(\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{100}{0,1}}=10\pi\left(rad/s\right)\)
\(\Rightarrow\upsilon=\pm\omega\sqrt{A^2-x^2}=\pm10\pi\sqrt{4^2-2^2}=\pm20\pi\sqrt{3\left(cm/s\right)}\)
Chúc bạn học tốt