Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn:
+ Độ biến dạng của lò xo tại vị trí cân bằng tạm x 0 = μ m g k = 0 , 1.0 , 1.10 100 = 10 − 3 m
→ Biên độ dao động của vật trong nửa chu kì đầu tiên A 1 = X 0 – x 0 .
Cứ sau mỗi nửa chu kì, kể từ nửa chu kì thứ 2 biên độ của vật dao động so với các vị trí cân bằng tạm sẽ giảm 2 x 0 .
→ Ta xét tỉ số A 1 2 x 0 = X 0 − x 0 2 x 0 = 0 , 1 − 10 − 3 2.10 − 3 = 49 , 5
→ Biên độ của vật sau 49 nửa chu kì tiếp theo là A 49 = A 1 – ( 49 . 2 + 1 ) x 0 = 1 m m → vật tắt dần tại đúng vị trí lò xo không biến dạng.
+ Áp dụng định luật bảo toàn và chuyển hóa năng lượng ta có 1 2 k X 0 2 = μ m g S → S = k X 0 2 2 μ m g = 100.0 , 1 2 2.0 , 1.0 , 1.10 = 5 m
Đáp án B

Hướng dẫn: Chọn đáp án C
Cách 1: Độ giảm cơ năng đúng bằng công của lực ma sát:

![]()
Cách 2: Xem I là tâm dao động và biên độ A 1 = A - x 1 , tốc độ tại O:
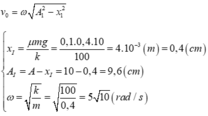
![]()

Hướng dẫn: Chọn đáp án A
![]()
![]()
Sau khi qua O lần 3, biên độ còn lại:

![]()

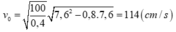
Bình luận: Đến đây, các bạn tự mình rút ra quy trình giải nhanh và công thức giải nhanh với loại bài toán tìm tốc độ khi đi qua O lần thứ n! Với bài toán tìm tốc độ ở các điểm khác điểm O thì nên giải theo cách 2 và chú ý rằng, khi đi từ P đến Q thì I là tâm dao động còn khi đi từ Q đến P thì I’ là tâm dao động.

Đáp án D
Phương pháp: Sử dụng lí thuyết về bài toán dao động tắt dần của con lắc lò xo
Cách giải:
Khi vật dừng lại, toàn bộ cơ năng chuyển thành công của lực ma sát:
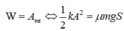
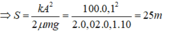
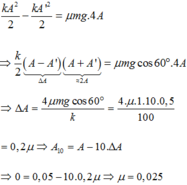
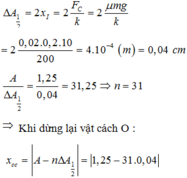


Chọn đáp án B
+ Sau 10 dao động vật dừng lại như vậy có 20 lần qua VTCB
+ Độ giảm biên độ của vật sau một lần qua VTCB:
Mặt khác vật dao động tắt dần trên mặt phẳng nghiên nên ta có độ giảm biên độ sau một lần vật qua VTCB: