Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\begin{cases}\Delta l_1=l_1-l_0=\frac{g}{\omega^2_1}\\\Delta l_2=l_2-l_0=\frac{g}{\omega^2_2}\end{cases}\)\(\Rightarrow\frac{\omega^2_2}{\omega^2_1}=\frac{21-l_0}{21,5-l_0}=\frac{1}{1,5}\)\(\Rightarrow l_0=20\left(cm\right)\)
\(\Rightarrow\Delta l_1=0,01\left(m\right)=\frac{g}{\omega^2_1}\Rightarrow\omega_1=10\pi\left(rad/s\right)\)
KQ = 3,2 cm

ban đầu T=0,4s => omega = 5p i=> deta lo =4 cm
=> t= T/4+T/4+T/12=7T/12=7/30s

Cái này hình như bạn viết nhầm đơn vị của g phải là m/s2
Khi lò xo có chiều dài l=28 thì vận tốc bằng 0=> vật ở vị trí biên âm
△l=|△l0-A|=2cm
Fd=k|△l|=2N
=>k=100N/m
△l0=\(\dfrac{m.g}{k}\)=0,02(m)=2cm
=>A=4cm
W=1/2.k.A2=0,08j

Độ giãn của lò xo tại VTCB: \(\Delta l_0=\frac{9}{\omega^2}=2cm\)
Lực đàn hồi có độ lớn 1,5 N
\(F=k.\left(\Delta l\pm x\right)\Leftrightarrow1,5=50.\left(0,02\pm x\right)\)\(\Leftrightarrow\left[\begin{array}{nghiempt}x=1cm\\x=-1cm\end{array}\right.\)
Khoảng thời gian ngắn nhất vật đi qua hai vị trí mà lực đàn hồi F = 1,5 N là :
\(t=\frac{T}{12}+\frac{T}{12}=\frac{\pi}{30\sqrt{5}}=s\)
Đáp án C

\(T=2\pi\sqrt{\frac{\Delta l_0}{9}}=0,4s\)
\(\Rightarrow\Delta l_0=4=\frac{A\sqrt{2}}{2}\)
Thời gian lò xo không giãn là \(t=2t-\frac{A\sqrt{2}}{2}\Rightarrow-A=\frac{T}{4}=0,10\left(s\right)\)
Vậy D đúng

Tần số góc: \(\omega=\sqrt{\frac{K}{m}}=10\pi\left(rad\text{/}s\right)\)
Biên độ dao động của vật \(A=\sqrt{x^2+\left(\frac{v}{w}\right)^2}=6\left(cm\right)\)
Lò xo có độ nén cực đại tại biên âm:
\(\Rightarrow\) Góc quét \(=\pi\text{/}3+\pi=\omega t\Rightarrow t=2\text{/}15\left(s\right)\)
chọn B

Chọn trục toạ độ có gốc ở VTCB, chiều dương hướng sang phải.
Phương trình dao động tổng quát là: \(x=A\cos(\omega t+\varphi)\)
Theo thứ tự, ta lần lượt tìm \(\omega;A;\varphi\)
+ \(\omega=\sqrt{\dfrac{k}{m}}=20\sqrt 2(rad/s)\)
+ Biên độ A: \(A^2=x^2+\dfrac{v^2}{\omega^2}=3^2+\dfrac{(80\sqrt 2)^2}{(20\sqrt 2)^2}\)
\(\Rightarrow A = 5cm\)
+ Ban đầu ta có \(x_0=3cm\); \(v_0=-80\sqrt 2\) (cm/s) (do ta đẩy quả cầu về VTCB ngược chiều dương trục toạ độ)
\(\cos\varphi=\dfrac{x_0}{A}=\dfrac{3}{5}\); có \(v_0<0 \) nên \(\varphi > 0\)
\(\Rightarrow \varphi \approx0,3\pi(rad)\)
Vậy PT dao động: \(x=5\cos(20\sqrt 2+0,3\pi)(cm)\)

\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)
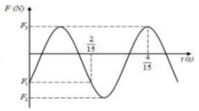

Giải thích: Đáp án A
Từ đồ thị ta thấy:
Lực đàn hồi tại thời điểm ban đầu: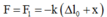
Lực đàn hồi tại vị trí biên dương:
Lực đàn hồi tại vị trí biên âm: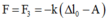
Gọi là thời gian từ t = 0 đến t = 2/15s
Ta có: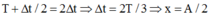
Theo đề bài: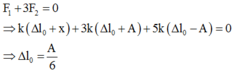
=> Thời gian lò xo nén là 0,446T
=> Thời gian lò xo giãn là 0,554T
Tỉ số thời gian lò xo giãn và lò xo nén trong một chu kì là 1,24
Chọn A