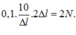Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B.
Do không thay đổi về k, m => ω không đổi.
→ ω = k m = 20 0 , 2 = 10 π ( r a d / s ) .
Ta có năng lượng truyền cho vật là:
E t r u y e n = 1 2 m v 2 = 1 2 .0 , 2.1 2 = 0 , 1 ( J )
⇒ 1 2 k A 2 = E t r u y e n = 0 , 1 ⇒ A = 0 , 1 ( m )
Khi tới biên A lần đầu, năng lượng còn lại là:
![]()
![]()
=> Biên độ còn lại:
![]()

Hướng dẫn:
Độ biến dạng của lò xo tại các vị trí cân bằng tạm x 0 = μ m g k = 0 , 01.0 , 2.10 20 = 1 m m
+ Tại vị trí lò xo không biến dạng → so với vị trí cân bằng tạm ở nửa chu kì đầu vật có x 1 = 1 m m .
→ Biên độ dao động trong nửa chu kì đầu là A 1 = x 1 2 + v 1 ω 2 = 1.10 − 3 2 + 1 10 2 ≈ 10 c m
→ Lực đàn hồi cực đại F d h m a x = k A 1 = 1 , 98 N .
Đáp án C

Gọi biên độ dao động là A.
Độ dãn của lò xo khi vật ở VTCB là: \(\Delta\ell_0=\dfrac{mg}{k}\)
Độ dãn cực đại của lò xo là: \(\Delta\ell_0+A=10cm=0,1m\)
Lực đàn hồi cực tiểu là: \(k(\Delta\ell_0-A)=0,8\)
\(\Rightarrow k(\Delta \ell_0+\Delta\ell_0-0,1)=0,8\)
\(\Rightarrow k(2\Delta \ell_0-0,1)=0,8\)
\(\Rightarrow k(2\dfrac{mg}{k}-0,1)=0,8\)
\(\Rightarrow2.mg-0,1.k=0,8\)
\(\Rightarrow2.0,24.10-0,1.k=0,8\)
\(\Rightarrow k=40(N/m)\)
Lực mà lò xo tác dụng lên vật khi lò xo dãn 5cm là lực đàn hồi của lò xo và bằng: \(F=k.\Delta\ell=40.0,05=2(N)\)


Đáp án B
Fdhmax = k(∆l + A) → Fdhmax = mω2(∆l + ∆l)
↔ Fdhmax =