Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Một con lắc lò xo dao động theo phương trình x = 4cos10t
\(W_t=W=\frac{1}{2}k.A^2=\frac{1}{2}m.w^2.A^2=8.10^{-3}=8\left(mJ\right)\)
Vậy C đúng
Thế năng cực đại của con lắc lò xo:
\(W_t=W=\frac{1}{2}k.A^2=\frac{1}{2}.m.\omega^2.A^2=8.10^{-3}=8mJ\)
Chọn C

–Năng lượng lúc đầu: 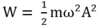
– Năng lượng lúc sau: 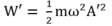
- Vì sau mỗi chu kỳ: A’ = (100 – 2,5)%A = 0,975A
- Suy ra:
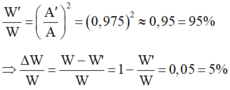

Gia tốc biểu kiến của con lắc trong thang máy là
\(\overrightarrow{g'} =\overrightarrow{g} -\overrightarrow{a} \)
Thang máy đứng yên: \(\overrightarrow{a} = 0; W= \frac{1}{2}kA^2= 0,5 m\omega^2g.(1) \)
Thang máy chuyển động nhanh dần đều đi lên gia tốc \(2,5 m/s\) => \(\overrightarrow{g} \uparrow \downarrow \overrightarrow{a} \)
=> \(g' = g-(-a)= g+a.\)
=> \(W' = \frac{1}{2}m\omega'^2.A^2.(2)\)
Chia (1) cho (2) ta có: \(\frac{W}{W'} = \frac{\omega ^2}{\omega'^2}= \frac{T'^2}{T^2}= \frac{g}{g'}= \frac{9,8}{12,3}=> W'= \frac{12,3.150}{9,8}=188,2mJ.\)
Chọn đáp án.B.188,2mJ.

+ Cơ năng của con lắc là: W = 1 2 k x 2 + 1 2 m v 2 = 1 2 k 0 , 045 − Δ l 2 + 1 2 m v 2
+ Mà Δ l = m g k
® 2 W = k 0 , 045 − m g k 2 + m .0 , 4 2 = 80.10 − 3
+ Giải phương trình trên ta được: m = 0 , 25 g m = 0 , 49 g ® chọn m = 0 , 25 g
+ T = 2 π m k = 2 π 0 , 25 100 = π 10 s
Đáp án B

ü Đáp án B
+ Cơ năng của con lắc là:
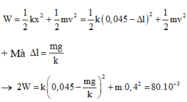
+ Giải phương trình trên ta được: m = 0 , 25 m = 0 , 49 → c h ọ n m = 0 , 25
T = 2 π m k = 2 π 0 . 25 100 = π 10 s

+ Cơ năng của con lắc là:

+ Mà ∆ l = m g k
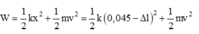
+ Giải phương trình trên ta được: m = 0 , 25 m = 0 , 49 → chọn m = 0,25 g
T = 2 π m k = 2 π 0 . 25 100 = π 10 s
ü Đáp án B

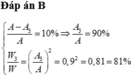
Đáp án A
Để duy trì dao động cho con lắc thì cơ năng của con lắc giảm bao nhiêu thì phải bù đắp bấy nhiêu
=> Năng lương̣ cần bổsung sau mỗi chu kì là 5mJ