Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

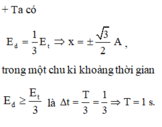
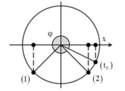
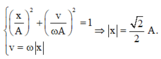
+ Tại t=0, vật đi qua vị trí x = 3 2 A , theo chiều dương. Biểu diễn các vị trí tương ứng trên đường tròn.
+ Trong một chu kì vật đi qua vị trí thỏa mãn yêu cầu bài toán 2 lần → tách 2016 = 2014+2
Vậy tổng thời gian là
![]()
Đáp án B

Đáp án B
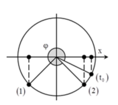
Ta có E d = 1 3 E t ⇒ x = ± 3 2 A trong một chu kì thời gian E d ≥ 1 2 E t là
∆ t = T 3 = 1 3 ⇒ t = 1 s
Kết hợp với
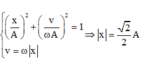
Tại t = 0 vật đi qua vị trí x = 3 2 A theo chiều dương. Biễu diễn các vị trí tương ứng trên đường tròn
Trong 1 chu kì đi qua vị trí thỏa mãn yêu cầu bài toán 2 lần → tách 2016 = 2014 +2
Vậy tổng thời gian là ∆ t = t φ + 1007 T = 23 24 + 1007 = 1007 , 958 s

Khoảng thời gian giữa 2 lần liên tiếp động ăng bằng thế năng là T/4
\(\Rightarrow \dfrac{T}{4}=\dfrac{\pi}{40}\)
\(\Rightarrow T = \dfrac{\pi}{10}\)
\(\Rightarrow \omega=\dfrac{2\pi}{T}=20(rad/s)\)
Biên độ dao động: \(A=\dfrac{v_{max}}{\omega}=\dfrac{100}{20}=5(cm)\)
Ban đầu, vật qua VTCB theo chiều dương trục toạ độ \(\Rightarrow \varphi=-\dfrac{\pi}{2}\)
Vậy PT dao động là: \(x=5\cos(20.t-\dfrac{\pi}{2})(cm)\)

Đáp án B
Ta có E d = 1 3 E t → x = ± 3 2 A trong một chu kì khoảng thời gian E d ≥ E t 3 là Δ t = T 3 = 1 3 s → T = 1 s.
Kết hợp với: x A 2 + v ω A 2 = 1 v = ω x → x = 2 2 A
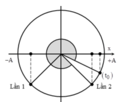
Tại t = 0, vật đi qua vị trí x = 3 2 A , theo chiều dương. Biểu diễn các vị trí tương ứng trên đường tròn
Trong một chu kì vật đi qua vị trí thoãn mãn yêu cầu bài toán 2 lần → tách 2016 = 2014 + 2
Vậy tổng thời gian là Δ t = t φ + 1007 T = 23 24 + 1007 = 1007 , 958 s

Bài này có vẻ lẻ quá bạn.
\(W_t=4W_đ\Rightarrow W_đ=\dfrac{W_t}{4}\)
Cơ năng: \(W=W_đ+W_t=W_t+\dfrac{W_t}{4}=\dfrac{5}{4}W_t\)
\(\Rightarrow \dfrac{1}{2}kA^2=\dfrac{5}{4}.\dfrac{1}{2}kx^2\)
\(\Rightarrow x = \pm\dfrac{2}{\sqrt 5}A\)
M N O α α
Thời gian nhỏ nhất ứng với véc tơ quay từ M đến N.
\(\cos\alpha=\dfrac{2}{\sqrt 5}\)\(\Rightarrow \alpha =26,6^0\)
Thời gian nhỏ nhất là: \(\Delta t=\dfrac{26,6\times 2}{360}.T=\dfrac{26,6\times 2}{360}.\dfrac{2\pi}{20}=0.046s\)

Áp dụng công thức: \(A^2 = x^2 +\frac{v^2}{\omega^2} \) \(\Rightarrow A^2 = 3^2 +\frac{(60\sqrt3)^2}{\omega^2} = (3\sqrt2)^2 +\frac{(60\sqrt2)^2}{\omega^2} \)
Giải hệ trên ta được \(\omega = 20rad/s; \ A =6cm\)

\(\omega_1=\frac{2\pi}{T_1}=\frac{10\pi}{3}\); \(\omega_2=\frac{2\pi}{T_2}=\frac{10\pi}{9}\)
\(\varphi_2=\omega_2t;\omega_1t=\pi-\varphi_2\)
\(\Rightarrow t=\frac{\pi}{\omega_1+\omega_2}=0,225\left(s\right)\)
 chọn A
chọn A
Đáp án B