
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Thời gian quả cầu đi từ vị trí cao nhất (x = -A) đến vị trí thấp nhất (x = A) chính là \(\frac{T}{2} = 0,2 => T = 0,4s.\)
Lực đàn hồi của lò xo khi lò xo ở vị trí thấp nhất chính là \(F_{dhmax} = k(A+\Delta l)\)
\(\frac{F_{max}}{P} = \frac{k(A+\Delta l)}{mg} = \frac{kA+k\Delta l }{mg } = 1+\frac{kA}{mg} =\frac{7}{4}\) (do \(k\Delta l = mg\))
=> \(A = \frac{3g}{4}\frac{m}{k} = \frac{3g}{4}.\frac{T^2}{4\pi^2} =0,03m = 3cm.\)

Độ biến dạng của lò xo khi vật ở VTCB là: \(\Delta \ell_0=\dfrac{mg}{k}=\dfrac{1.10}{100}=0,1m=10cm\)
\(\omega=\sqrt{\dfrac{k}{m}}=10(rad/s)\)
Áp dụng CT: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow A^2=2^2+\dfrac{(20\sqrt 3)^2}{10^2}\)
\(\Rightarrow A = 4cm\)
Lực đàn hồi cực đại:
\(F_{dhmax}=k\Delta\ell_{max}=k(\Delta\ell_0+A)=100.(0,1+0,04)=14(N)\)
Lực đàn hồi cực tiểu:
\(F_{dhmin}=k\Delta\ell_{min}=k(\Delta\ell_0-A)=100.(0,1-0,04)=6(N)\)

Đáp án B
Phương pháp: Sử dụng lí thuyết về con lắc lò xo dao động điều hòa theo phương thẳng đứng
Cách giải:
+ Tần số góc ω = 2 π T
+ Độ giãn của lò xo ở VTCB:
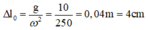
+ Do ∆ l 0 < A nên lực đàn hồi của lò xo có độ lớn cực tiểu bằng 0 tại vị trí lò xo không biến dạng
=> Thời gian vật đi từ VTCB (x = 0) đến VT lò xo không biến dạng (x = -4 cm) là t = T/12 = 1/30 s
=> Chọn B