Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gia tốc biểu kiến của con lắc nằm trong thang máy chuyển động với gia tốc \(\overrightarrow a\) là:
\(\overrightarrow {g'} = \overrightarrow {g} -\overrightarrow a \)
Thang máy đi lên chậm dần đều nên \(\overrightarrow g \uparrow \uparrow \overrightarrow a\) => \( {g'} ={g} -a \)
Mà \(a = \frac{g}{2} => g' = g - \frac{g}{2} = \frac{g}{2}.\)
Chu kì của con lắc lúc này là \(T' =2\pi \sqrt{\frac{l}{g}} = 2\pi \sqrt{\frac{2l}{g}} = T\sqrt{2}.\)
Chắc là C quá.
Theo mình thì VTCB chỉ có lực căng dây cực đại.Hợp lực cực đại khi chắc là ở biên.
Gia tốc của vật nặng là gia tốc hướng tâm vì nó chuyển động tròn đều nên không hướng về VTCB.
Chọn gốc thế năng tại VT dây thẳng đứng.
Áp dụng định luật bảo toàn năng lượng ta có:
\(W=mgl\left(1-\cos\alpha_0\right)=W_d+W_t=W_d+mgl\left(1-\cos\alpha\right)\)
\(\Rightarrow W_d=mgl\left(1-\cos\alpha_0-1+\cos\alpha\right)=mgl\left(\frac{\alpha^2_0}{2}-\frac{\alpha^2}{2}\right)\)
\(=0,1.10.0,8.\left(\frac{\left(\frac{8}{180}\pi\right)^2-\left(\frac{4}{180}\pi\right)^2}{2}\right)\approx5,84\left(mJ\right)\)
Đáp án B
Phương pháp: Sử dụng công thức tính lực căng dây của con lắc đơn dao động điều hòa
Cách giải:
+ Biên độ dao động của con lắc: α 0 = 6 0 = π / 30 rad
+ Khi con lắc ở vị trí có
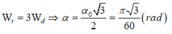
=> Lực căng dây của con lắc:
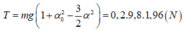
=> Chọn D
Ta có: \(v=\omega\sqrt{s^2_0-s^2}=\sqrt{gl\left(\alpha^2_0-a^2_1\right)}\)\(=0,271\left(m\right)=27,1\left(cm\text{/}s\right)\)
=2 7,1 cm/s
Lực căng dây cực tiểu tại vị trí biên:
\(T_{min}=mg(3.\cos\alpha_0-2\cos\alpha_0)=mg.\cos\alpha_0\)
\(\Rightarrow 0,2.10.\cos\alpha_0=1\)
\(\Rightarrow \alpha_0=60^0\)
Tại vị trí thế năng bằng động năng thì cơ năng là: \(W=W_t+W_đ=2W_t\)
\(\Rightarrow mgl(1-\cos\alpha_0)=2.mgl(1-\cos\alpha)\)
\(\Rightarrow \cos\alpha=\dfrac{1+\cos\alpha_0}{2}=\dfrac{3}{4}\)
\(\Rightarrow \alpha=41,4^0\)
Lực căng dây: \(T=mg(3\cos\alpha-2\cos\alpha_0)=0,2.10.(3.\dfrac{3}{4}-2.\dfrac{1}{2})=2,5(N)\)
Lực căng dây: \(T=mg(3\cos \alpha-2\cos \alpha_0)\)
Lực căng dây cực đại ở VTCB: \(T_{max}=mg(3-2\cos \alpha_0)=1\)
\(\Rightarrow 0,2.10.(3-2\cos \alpha_0)=1\)
\(\Rightarrow \cos\alpha_0=\dfrac{5}{4}\), vô lý
Bạn xem lại đề nhé.
\(W_t=\frac{mgl\alpha^2}{2}=\frac{4.1,2.0,05^2}{2}=6.10^{-3}J\)
Chọn D
Thế năng: Et = mghB = mgl(1 - cosa)
Năng lượng: E =Et max= mghmax= mgll.(1 - cosa0)
(Năng lượng bằng thế năng cực đại ở biên)
- Động năng:
Xét tại vị trí B, hợp lực tác dụng lên quả nặng là lực hướng tâm: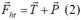
(ở đây ký hiệu T là lực căng)
Thế R = l và (1) vào (3) ta được T = mg(3cosa - 2cosa0)
Khi Eđ = 2Et → Et = E/3 ↔ mgl(1 - cosa) = mgl.(1 - cosa0)/3→cosα = (2 + cosα0)/3
→ T = mg(2 – cosa0).