Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có: \(\omega=\sqrt{\dfrac{g}{l}}=\dfrac{5\pi}{4}\left(\dfrac{rad}{s}\right)\)
\(\rightarrow A=\dfrac{v_{max}}{\omega}=\dfrac{0,4}{\dfrac{5\pi}{4}}=\dfrac{8\pi}{25}\left(m\right)\)
\(t:0\left\{{}\begin{matrix}x=0\\v>0\end{matrix}\right.\Rightarrow\varphi=-\dfrac{\pi}{2}\left(rad\right)\)
\(\rightarrow v=-4sin\left(\dfrac{5\pi}{4}t-\dfrac{\pi}{2}\right)\left(\dfrac{m}{s}\right)\)
Thay t = 2 vào \(\Rightarrow v=0\left(\dfrac{m}{s}\right)\)
\(S=l.\alpha_0\Rightarrow\alpha_0=\dfrac{4}{100}=0,04\left(rad\right)\)
\(\omega=\sqrt{\dfrac{g}{l}}=\pi\left(rad/s\right)\)
\(\Rightarrow\alpha=0,04\cos\left(\pi t-\dfrac{\pi}{2}\right)\left(rad\right)\)
\(S=4\cos\left(\pi t-\dfrac{\pi}{2}\right)\left(cm\right)\)
Chọn đáp án D
Con lắc đơn dao động điều hòa nên ta có:
v ω A 2 − x 2 = g l α 0 2 l 2 − α 2 l 2 = g l α 0 2 − α 2 α = 0 ⇒ v = α 0 g l
Đáp án D
+ Chu kì dao động của con lắc T = π l g + π 0 , 5 l g = π 1 π 2 + π 0 , 5 π 2 = 1 + 2 2 s
Từ hệ thức độc lập thời gian giữa li độ dài và vận tốc:
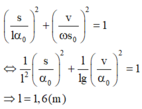
Đáp án C
x = S 0 cos φ = 0 ⇒ cos φ = 0
v = - S 0 ωsin φ > 0 ⇒ sin φ < 0
⇒ φ = - π /2
ω = 2 π /T = 2 π /2 = π rad/s
s = 6cos( π t - π /2)cm
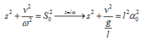
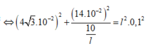
Tần số góc của dao động con lắc đơn:
\(\omega= \sqrt{\dfrac{g}{\ell}}= \sqrt{\dfrac{\pi^2}{1}}=\pi(rad/s)\)
Biên độ: \(A=\dfrac{v_{max}}{\omega}=\dfrac{0,5}{\pi}(m/s)=\dfrac{50}{\pi}(cm/s)\)
Lúc t = 0 con lắc đi qua VTCB theo chiều dương suy ra pha ban đầu: \(\varphi=-\dfrac{\pi}{2}(rad/s)\)
Suy ra PT li độ: \(x=\dfrac{50}{\pi}\cos(\pi t-\dfrac{\pi}{2})(cm)\)
PT vận tốc: \(v=x'_{t}=-50.\sin(\pi t -\dfrac{\pi}{2})(cm/s)\)
Tại thời điểm \(t=2,5s\) vận tốc của con lắc là:
\(v=-50.\sin(\pi . 2,5 -\dfrac{\pi}{2})(cm/s)=0(cm/s)\)