Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

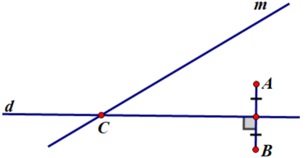
Gọi A và B là hai điểm dân cư, C là điểm đặt trạm y tế.

Vì C cách đều AB nên C thuộc đường trung trực của AB mà C ∈ xy nên C là giao điểm của xy và đường trung trực của AB
gọi 2 điểm dân cư đó là A và B, trạm y tế là C.
để C cách đểu A và B thì C phải thuộc đường trung trực của AB.
khi đó để được điểm C nằm trên đường quốc lộ và cách đều 2 điểm A,B thì C phải trùng với giao điểm của đường trung trực của AB và đường quốc lộ.
vậy trạm y tế được đặt ở giao điểm của đường quốc lộ và đường trung trực của AB.

Gọi A và B là hai điểm dân cư ; C là điểm đặt trạm y tế ; m là đường quốc lộ
Vì C cách đều AB nên C thuộc đường trung trực của AB
mà C ∈ d nên C là giao điểm của d và đường trung trực (d) của AB.
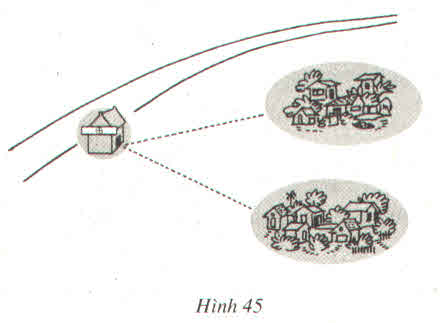
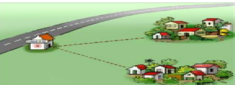
Gọi 2 điểm dân cư là hai điểm A, B. Để xây dựng trạm y tế ở bên đường cách đều hai điểm dân cư thì trạm y tế đó phải là giao điểm giữa con đường và đường trung trực của AB.

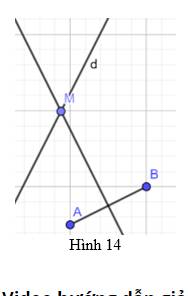
Để M cách đều A, B khi và chỉ khi M thuộc trung trực của đoạn AB
Vì M phải thuộc d \( \Rightarrow \) M là giao điểm của trung trực AB và đường thẳng d

Ta có:
\(AC+BC\ge AB\) ( vì \(C\)là điểm chưa xác định )
Do đó:
\(AC+BC\)ngắn nhất khi:
\(AC+BC=AB\)
\(\Rightarrow C\)nằm giữa \(AB\)
Vậy vị trí đặt một cột mắc dây điện từ trạm về cho khu dân cư sao cho độ dài đường dây ngắn nhất là \(C\)nằm giữa \(AB\)
Ta có: AC + BC ≥ AB ( vì C là điểm chưa xác định)
Do đó : AC + BC ngắn nhất khi:
AC + BC = AB
=> C nằm giữa A và B
Vậy vị trí đặt một cột mắc dây điện từ trạm về cho khu dân cư sao cho độ dài đường dây dẫn ngắn nhất là C nằm giữa A và B

Để độ dài đường dây là ngắn nhất thì C nằm trên đoạn thẳng AB, tức là:
AC + BC = AB.
Thật vậy, nếu C nằm ngoài đoạn thẳng AB thì ba điểm A, B, C tạo thành một tam giác ABC. Theo định lý tổng hai cạnh trong tam giác ta có:
AC + BC > AB
Vậy để độ dài đường dây là ngắn nhất thì C nằm trên đoạn thẳng AB.
Để độ dài đường dây là ngắn nhất thì C nằm trên đoạn thẳng AB, tức là:
AC + BC = AB.
Thật vậy, nếu C nằm ngoài đoạn thẳng AB thì ba điểm A, B, C tạo thành một tam giác ABC. Theo định lý tổng hai cạnh trong tam giác ta có:
AC + BC > AB
Vậy để độ dài đường dây là ngắn nhất thì C nằm trên đoạn thẳng AB

Gọi A và B là hai điểm dân cư, C là điểm đặt trạm y tế.
Vì C cách đều AB nên C thuộc đường trung trực của AB mà C ∈ xy nên C là giao điểm của xy và đường trung trực của AB
còn câu cách bao xa mk chưa bt lm nhaaaaaaaaaaaaaa![]()

Hướng dẫn
Ta có: AC + BC ≥ AB ( vì C là điểm chưa xác định)
Do đó : AC + BC ngắn nhất khi:
AC + BC = AB
=> C nằm giữa A và B
Vậy vị trí đặt một cột mắc dây điện từ trạm về cho khu dân cư sao cho độ dài đường dây dẫn ngắn nhất là C nằm giữa A và B
Vậy................
.jpg)
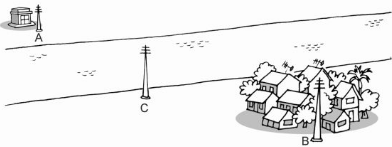

Gọi A và B là hai điểm dân cư ; C là điểm đặt trạm y tế ; m là đường quốc lộ
Vì C cách đều AB nên C thuộc đường trung trực của AB
mà C ∈ xy nên C là giao điểm của xy và đường trung trực (d) của AB.
Gọi 2 điểm dân cư là hai điểm A, B. Để xây dựng trạm y tế ở bên đường cách đều hai điểm dân cư thì trạm y tế đó phải là giao điểm giữa con đường và đường trung trực của AB.