Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trong một hệ kín, nếu có một phần của hệ chuyển động theo một hướng thì theo định luật bảo toàn động lượng, phần còn lại của hệ phải chuyển động theo hướng ngược lại. Chuyển động theo nguyên tắc như trên gọi là chuyển động bằng phản lực.
-> Chuyển động của một con cá đang bơi là chuyển động bằng phản lực.
Vậy đáp án là D.

Đáp án C.
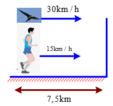
Con chim và vận động viên chuyển động cùng thời gian khi đến đích:


Chọn đáp án C
? Lời giải:
+ Con chim và vận động viên chuyển động cùng thời gian khi đến đích: t = s v = 7 , 5 15 = 0 , 5 h
+ Quãng đường di chuyển của con chim: s = 30.0 , 5 = 15 k m

Đáp án C.
Con chim và vận động viên chuyển động cùng thời gian khi đến đích: t = s v = 7 , 5 15 = 0 , 5 h
Quãng đường di chuyển của con chim: s = 30.0 , 5 = 15 k m

m=250g=0,25kg
a) gốc thế năng tại mặt đất (h=800m)
\(W_t=m.g.h\)=2000J
b) gốc thế năng tại đỉnh núi cao 500m (h=300m)
\(W_t=m.g.h\)=750J
c) đỉnh núi cao 1200m (h=-400m)
\(W_t=m.g.h\)=-1000J
d) mặt biển dưới đât 200m (h=1000m)
\(W_t=m.g.h\)=2500J

Gọi:
+ Khối lượng, vận tốc trước và sau va chạm của chim đại bàng lần lượt là m1 , v1 , v’1
+ Khối lượng, vận tốc trước và sau va chạm của chim bồ câu lần lượt là m2 , v2 , v’2
Do va chạm của chim đại bàng và chim bồ câu là va chạm mềm nên ta có v’1 = v’2 = v’
Ta có: m1 = 1,8 kg; m2 = 0,65 kg; v1 = 18 m/s; v2 = 7 m/s
Chọn chiều dương là chiều chuyển động của chim đại bàng.
Áp dụng định luật bảo toàn động lượng, ta có:
\(\begin{array}{l}\sum {\overrightarrow {{p_{tr}}} = \sum {{{\overrightarrow p }_s}} } \\ \Leftrightarrow {m_1}.\overrightarrow {{v_1}} + {m_2}.\overrightarrow {{v_2}} = ({m_1} + {m_2}).\overrightarrow {v'} \end{array}\)
Chiếu lên chiều dương, ta có:
\(\begin{array}{l}{m_1}.{v_1} + {m_2}.{v_2} = ({m_1} + {m_2}).v'\\ \Rightarrow v' = \frac{{{m_1}.{v_1} + {m_2}.{v_2}}}{{{m_1} + {m_2}}} = \frac{{1,8.18 + 0,65.7}}{{1,8 + 0,65}} \approx 15,08(m/s)\end{array}\)
Vậy tốc độ của chúng ngay sau khi chim đại bàng bắt được bồ câu là 15,08 m/s.


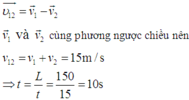



Chim mẹ chuyển động so với chim con nhưng đứng yên so với con mồi