Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B 0 5cm -5cm 3cm
Áp dụng định luật bảo toàn năng lượng
Vật đi từ A được 2 cm tức là vật đang có li độ x = 3 cm.
\(W_{A,x=5cm } = W_{B,x=3cm}\)
=> \(\frac{1}{2}kx_0^2 = A_{F_{ms}}+\frac{1}{2}mv_1^2+\frac{1}{2}kx_1^2\)
=> \(\frac{1}{2}k(x_0^2-x_1^2) = F_{ms}S+\frac{1}{2}mv_1^2\)
=>\(\frac{1}{2}mv_1^2= \frac{1}{2}k(x_0^2-x_1^2) - \mu mgS\)
=>\(\frac{1}{2}mv_1^2= \frac{1}{2}100(0,05^2-0,03^2) - 0,25.1. 10. 0,02\)
=> \(\frac{1}{2}mv^2 = 0,03\)
=> \(v = \sqrt{\frac{2.0,03}{1}} = 0,245 m/s.\)
Mình nghĩ là kết quả là 0,245 m/s.

Chọn C

+ Độ giảm biên độ trong nửa chu kì: ![]()
+ Theo yêu cầu của đề: 0,04 + (0,04 – ΔA) < S < 0,04 + 2(0,04 – ΔA)
=> 0,08 – 0,4μ < S < 0,12 – 0,8μ
+ Tới khi dừng hẳn: ![]()
+ 0,08 – 0,4μ < 4.10-3 /μ => (μ – 0,1)2 > 0
+ 4.10-3 /μ < 0,12 – 0,8μ => μ2 – 0,15μ + 0,005 < 0 => 0,05 < μ < 0,1.

Đáp án B
Nên nhớ các công thức trong dao động tắt dần:
Quãng đường vật đi được đến khi dừng hẳn: s = k A 2 2 μ m g
Thay số vào ta được: s = 10 . 0 , 07 2 2 . 0 , 1 . 0 , 1 . 10 = 0 , 245 m = 24 , 5 c m

- Nên nhớ các công thức trong dao động tắt dần:
- Quãng đường vật đi được đến khi dừng hẳn:
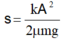
Thay số vào ta được:
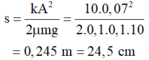

Hướng dẫn: Chọn đáp án D
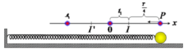
Khoảng cách:
![]()
Thời gian ngắn nhất vật đi từ P đến điểm O là
![]()
Tốc độ trung bình trong khoảng thời gian đó:
![]()

Hướng dẫn:
+ Vật m 2 sẽ rời khỏi m 2 khi hai vật này đi qua vị trí cân bằng tạm lần đầu tiên
→ Tốc độ của vật m 2 tại vị trí này
v 0 = ω X 0 − x 0 = k m 1 + m 2 X 0 − μ m 1 + m 2 g k = 50 0 , 1 + 0 , 4 0 , 1 − 0 , 05 0 , 1 + 0 , 4 .10 50 = 0 , 95
+ Quãng đường m 2 đi được từ khi rời vật m 1 đến khi dừng lại 1 2 m 2 v 0 2 = μ m 2 g S → S = v 0 2 2 μ g = 0 , 9025 m
→ Vậy tổng thời gian từ khi thả vật m 2 đến khi m 2 dừng lại là t = T 4 + 2 S μ g = 2 , 056 s
Đáp án C

Đáp án A
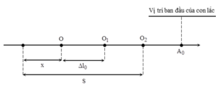
+ Gọi Δ l 0 là độ biến dạng của lò xo ứng với cường độ điện trường có độ lớn E
Cứ mỗi lần điện trường tăng lên một lượng E thì vị trí cân bằng của con lắc dịch chuyển về phía phải một đoạn Δ l 0 và biên độ sẽ giảm đi một lượng cũng đúng bằng Δ l 0 .Trong 4 s khi đó vị trí cân bằng của con lắc bây giờ trùng với vị trí ban đầu do đó con lắc sẽ dừng lại không dao động nữa
A 0 = 3 Δ l 0 4 A 0 − 2 Δ l 0 + 4 A 0 − Δ l 0 = 3 S → S = 4 3 A 0
Kết hợp với x A 0 2 + v ω A 0 2 = 1 → A 0 = 9 S = 12 c m

Với bài toán dạng này, khi áp dụng định lý biến thiên cơ năng chúng ta thường lấy gần đúng là vật dừng lại ở VTCB, khi đó cơ năng lúc sau = 0.
Nhưng nếu tính một cách chính xác thì không phải, vật dừng lại khi hợp lực tác dụng lên nó = 0, lúc đó Fđh = Fms, ta giả sử vật dừng lại ở li đô x thì: \(k.x=\mu mg\Rightarrow x=\frac{\mu mg}{k}\)
Lúc đó, công thức biến thiên cơ năng phải là: \(\frac{1}{2}k.A^2-\frac{1}{2}k.\left(\frac{\mu mg}{k}\right)^2=\mu mg.S\)
Từ đó, bạn rút ra S.