Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tần số \(f=\dfrac{\omega}{2\pi}=2,5(hz)\)
Như vậy, khi biểu diễn dao động bằng véc tơ quay thì trong giây đầu tiên véc tơ quay đã quay 2,5 vòng.
O x M 6 3 4 N P
Véc tơ quay xuất phát từ M quay ngược chiều kim đồng hồ, trong giây đầu tiên, nó quay 2,5 vòng
Ta thấy nó qua N, P tổng cộng 4 lần nên dao động điều hòa qua x = 4cm 4 lần.

4 x O -4 M0 M1 M2 -2
Chu kì dao động: T = 2π/(2π/3) = 3s
Véc tơ quay biểu diễn dao động trên xuất phát từ M0 và quay ngược chiều kim đồng hồ.
Cứ mỗi lần véc tơ quay đi qua M1 và M2 thì dao động điều hòa của chất điểm lại qua vị trí -2cm.
+ Véc tơ quay quay được 1005 vòng thì chất điểm qua -2cm số lần là: 1005 x 2 = 2010 lần.
+ Lần cuối cùng chất điểm qua -2cm ứng với véc tơ quay từ M0 đến M1, với góc quay: 90 + 30 = 1200
Vậy thời điểm chất điểm qua li độ -2cm lần 2011 là: 1005T + 120/360 T = (1005+1/3)T = (1005 + 1/3). 3 = 3016 s

Tần số f = 2,5 Hz.
Biểu diễn dao động bằng véc tơ quay ta có:
3 -3 M 1 -1 O x N
Do pha ban đầu bằng \(-\frac{2\pi}{3} \) nên chất véc tơ quay xuất phát từ M, quay được 2,5 vòng (ứng với 2,5Hz) trong một giây. Nhận thấy hình chiếu của M qua li độ 1cm 4 lần trong 2 vòng đầu, nửa vòng cuối quay chỉ đến N nên hình chiếu chưa qua li độ 1 cm. Do vậy dao động qua li độ 1cm là 4 lần trong giây đầu tiên.

Chọn A
Ta có T = 2 π ω = 2 π 5 π = 0,4 s. Biên độ A = 3 cm.
Có t = 1 s = 2,5 T = 2T + 0,5T.
Trong 1 chu kì vật đi qua vị trí x = +1 cm 2 lần.
Trong khoảng T/2 vật đi từ vị trí π/6 đến -5π/6 → vật đi qua vị trí x = +1 cm 1 lần.
Vậy trong giây đầu tiên vật đi qua vị trí x = +1 cm số lần n = 2.2 + 1 = 5 lần.

Chọn D
+ Chu kỳ dao động: ![]()
+ Chuyển về hàm số cos:
![]()
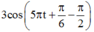

+ Vẽ vòng tròn lượng giác, t = 0 => x = 1,5 cm; v >0 => x đang tăng.
+ Với t = 1 (s): bán kính quay 2,5 vòng, đi qua các điểm có tọa độ x = +1 với số lần là 5.

Đáp án B

Chu kì dao động của chất điểm T = 0,4 s.
+ Ta có Δt = 10T + 0,5T = 4,2 s.
Trong mỗi chu kì có 1 lần vật đi qua vị trí x = – 5 cm theo chiều dương.
→ Trong 10T sẽ có 10 lần vật đi qua vị trí x = – 5 cm theo chiều dương.
Nửa chu kì còn lại vật đến vị trí x = – 5 cm theo chiềm âm.
→ Vậy kể từ thời điểm ban đầu, có 10 lần vật đi qua vị trí x = – 5 cm theo chiều dương.

Tỉ số cơ năng
\(\frac{W_1}{W_2}=\frac{k_1A_1^2}{k_2A_2^2}=\frac{m_1\omega_1^2A_1^2}{m_2\omega_2^2A_2^2}=\frac{50.\left(5\pi\right)^21^2}{100.\pi^2.5^2}=\frac{1}{2}\)

Cơ năng: \(W=\frac{1}{2}kA^2=\frac{1}{2}m\omega^2A^2\)
Suy ra: \(\frac{W_1}{W_2}=\frac{m_1\omega_1^2A_1^2}{m_2\omega_2^2A_2^2}=\frac{0,05.\left(5\pi\right)^2.0,01^2}{0,1.\left(\pi\right)^2.0,05^2}=\frac{1}{2}\)
Đáp án A

\(x=3\sin(5\pi t + \frac \pi 6) = 3\cos(5\pi t - \frac{\pi}{3}) \)(cm)
Tần số: f = 2,5Hz
Biểu diễn bằng véc tơ quay ta có:
3 -3 M 1 -1 O x
Véctơ quay xuất phát từ M, quay 2,5 vòng (ứng với 2,5Hz), khi đó, hình chiếu véc tơ quay qua -1cm là 5 lần.
Do vậy dao động qua li độ -1cm 5 lần trong 1s đầu tiên.
\(x=3\sin\left(5\pi t+\frac{\pi}{6}\right)=3\cos\left(5\pi t-\frac{\pi}{3}\right)\)(cm).
\(x_0=\frac{3}{2}=\frac{R}{2}\);\(T=\frac{2\pi}{5\pi}=\frac{2}{5}\left(s\right)\)
\(\Delta_t=1\left(s\right)=2T+\frac{T}{2}\)
*Xét 2T đầu: đi đc 4 lần.
*Xét \(\frac{T}{2}\) cuối:
\(x=-1=\frac{-R}{3}\)
0 R R/2 -R -R/3
Trong T/2, vật đi đc từ \(\frac{R}{2}\) đến \(\frac{-R}{2}\)
Vậy vật đi qua x=-1cm trong 1 s đầu tiên 5 lần.
#Walker