Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn đáp án B
Dựa vào đồ thị ta có:
T = 1 , 6 s ⇒ ω = 5 π 4 r a d / s ;
x = A cos 5 π 4 . t + π 8 c m
Tại thời điểm t = 0,2 s, chất điểm có li độ 2 cm suy ra:
2 = A cos 5 π 4 .0 , 2 + π 8 c m ⇒ A ≈ 5 , 2 c m
a = − ω 2 A . cos 5 π 4 . t + π 8
= − 5 π 4 2 .5 , 2. cos 5 π 4 .0 , 9 + π 8
= 57 c m / s 2
Đáp án B
Từ đồ thị ta có: T 2 = 1,1 – 0,3 = 0,8 (s) ð T = 1,6 s
ð w = 2 π t = 2 π 1 , 6 = 1,25π (rad/s); thời điểm t = 0,7 s thì
x = -A=Acos(1,25π.0,7 + j) ð cos(1,25π.0,7 + j) = - 1 = cosπ
ð j = π – 0,785π = π 8 ; thời điểm t = 0,2 s thì x = 2 = Acos(1,25π.0,2 + π 8 )
ð A = 5,226 (cm); thời điểm t = 0,9 s thì
a = - w2x = - (1,25π)2.5,226.cos(1,25π.0,9 + π 8 ) = 56,98679 (cm/s2).
Giải thích: Đáp án D
Phương pháp :
Sử dụng lí thuyết về dao động điều hoà kết hợp ki ̃năng đọc đồ thị viết phương trình của x
Thay t vào phương trình của v
Cách giải :
Ta có: 
Phương trình dao động: 
Thay t = 3s vào phương trình v ta thu được: v = -5,24 cm/s
Giải thích: Đáp án A
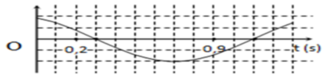
Phương pháp: Sử dụng phương trình li độ và gia tốc của dao động điều hòa, kết hợp kĩ năng đọc đồ thị.
Cách giải:
+ Phương trình của li độ và gia tốc: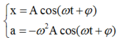
+ Từ đồ thị ta thấy: T/2 = 8 ô, 1 ô = 0,1s T = 1,6s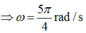
+ Tại t = 0,3s có x = 0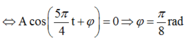
+ Tại t = 0,3s có x = 2cm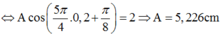
=> Phương trình của gia tốc: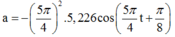
+ Tại t = 0,9s