


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





Đáp án B
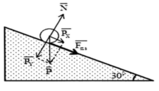
Trước hết ta tìm gia tốc a chuyển động của toa xe trên mặt phẳng nghiêng
Theo định luật II Niu-tơn :
Xét theo phương Oy vuông góc với mặt phẳng nghiêng :
Phản lực : N = mgcos α
Lực ma sát F = μ N = μ m g cos α
Xét theo phương Ox của mặt phẳng nghiêng thì :
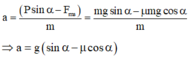
Với β = 90 0 - α ⇒ cos β = sin α , với F = ma
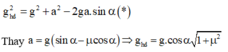
Chu kì dao động bé của con lắc đơn : T = 2 π 1 g hd = 2 π 1 gcosα 1 + μ 2
Từ những dữ kiện trên ta thay số vào tính được : v m a x = 0 , 21 m / s

Toa xe trượt không ma sát trên đường dốc với góc nghiêng \(\alpha\)
Ta có kết quả:
+ Khi vật ở VTCB thì phương của sợi dây vuông góc với mặt phẳng nghiêng.
+ Gia tốc hiệu dụng của vật: \(g'=g.\cos a\)
Chu kì dao động: \(T=2\pi\sqrt{\frac{l}{g'}}=2\pi\sqrt{\frac{1,5}{10.\cos45^o}}\approx2,89\left(s\right)\)

Toa xe trượt không ma sát trên đường dốc với góc nghiêng \(\alpha\)
Ta có kết quả:
+ Khi vật ở VTCB thì phương của sợi dây vuông góc với mặt phẳng nghiêng.
+ Gia tốc hiệu dụng của vật: \(g'=g.\cos\alpha\)
Chu kì dao động: \(T=2\pi\sqrt{\dfrac{\ell}{g'}}=2\pi\sqrt{\dfrac{1,5}{10.\cos 45^0}}\approx2,89(s)\)

Khoảng thời gian giữa 2 lần liên tiếp động ăng bằng thế năng là T/4
\(\Rightarrow \dfrac{T}{4}=\dfrac{\pi}{40}\)
\(\Rightarrow T = \dfrac{\pi}{10}\)
\(\Rightarrow \omega=\dfrac{2\pi}{T}=20(rad/s)\)
Biên độ dao động: \(A=\dfrac{v_{max}}{\omega}=\dfrac{100}{20}=5(cm)\)
Ban đầu, vật qua VTCB theo chiều dương trục toạ độ \(\Rightarrow \varphi=-\dfrac{\pi}{2}\)
Vậy PT dao động là: \(x=5\cos(20.t-\dfrac{\pi}{2})(cm)\)