Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

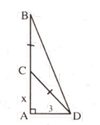
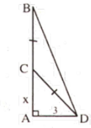
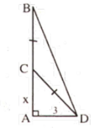
Giả sử AB là độ cao của cây tre, C là điểm gãy.
Đặt AC = x (0 < x < 9) => CB = CD = 9 – x.
Vì ∆ ACD vuông tại A
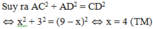
Vậy điểm gãy cách gốc cây 4m
Đáp án cần chọn là: C

Điểm gãy cách gốc \(\sqrt{8^2+3,5^2}=\dfrac{\sqrt{305}}{2}\approx8,73\left(m\right)\)


Giả sử AB là độ cao của cây tre, C là điểm gãy.
Đặt AC = x CB = CD = 8 – x.
Vì ∆ ACD vuông tại A
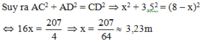
Vậy điểm gãy cách gốc cây 3,23m
Đáp án cần chọn là: B

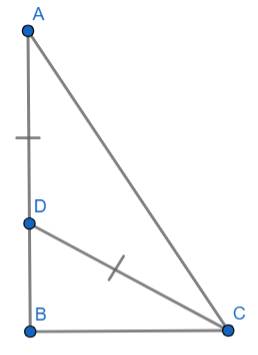
Ta cần tính khoảng cách từ điểm gẫy đề gốc cây tức là đoạn DB với đó C chính là điểm bị gẫy
Mà: \(AB=AD+DB\Rightarrow AD=AB-BD=8-DB\)
Và do AD là phần thân trên lúc chưa gẫy và DC là phân thân trên lúc đã gẫy nên
\(AD=DC=8-DB\)
Xét tam giác DBC vuông tại B áp dụng định lý Py-ta-go ta có:
\(DB^2+BC^2=CD^2\)
\(\Leftrightarrow DB^2+3,5^2=\left(8-DB^2\right)\)
\(\Leftrightarrow DB^2+12,25=64-16DB+DB^2\)
\(\Leftrightarrow DB^2-DB^2+16DB=64-12,25\)
\(\Leftrightarrow16DB=51,25\)
\(\Leftrightarrow DB=\dfrac{51,25}{16}\approx3,23\left(m\right)\)
Vậy khoảng cách từ điểm gẫy đến gốc dài 3,23 m

Giả sử gốc là điểm A, điểm gãy là B và điểm ngọn chạm đất là C, ta có tam giác ABC vuông tại A
Trong đó \(AC=3m\) ; \(AB+BC=9\left(m\right)\)
Áp dụng định lý Pitago:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow AB^2+3^2=\left(9-AB\right)^2\)
\(\Leftrightarrow9=81-18AB\)
\(\Rightarrow AB=4\left(m\right)\)
Vậy điểm gãy cách gốc 4m