Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
+ Khoảng cách giữa hai gợn lồi liên tiếp đúng bằng một bước sóng

Đáp án: A
HD Giải: λ = v f = 40 20 = 2 c m . Hai gợn lồi liên tiếp có đường kính chênh lệch nhau 2λ= 4cm

Bước sóng: \(\lambda = v/f = 40/20 = 2cm\)
Hai gợn lỗi liên tiếp có đường kính chênh lệch nhau bằng 1 bước sóng, và bằng 2cm.

Đáp án D
+ Ta có ∆ d = 8 λ = 30 - 14 = 16 c m → λ = 2 c m → Vận tốc truyền sóng v = λ f = 2.20 = 40cm/s

Khoảng cách ngắn nhất giữa hai gợn lồi liên tiếp là \(\frac{\lambda}{2} \Rightarrow \lambda = 2.2=4cm\)
Số gợn lồi (dao động cực đại) là số giá trị k thỏa mãn: \(-S_{1}S_{2}< k \lambda < S_{1}S_{2}\Rightarrow -4.125 < k < 4.125\\ \Rightarrow k = -4,-3,-2,-1,0,1,2,3,4\)
=> có 9 gợn lồi.
Số gợn lõm (dao động cực tiểu) là số giá trị k thỏa mãn: \(-S_{1}S_{2}< (k+0.5) \lambda < S_{1}S_{2}\Rightarrow -4.125 < k+0.5 < 4.125\\ \Rightarrow -4.625 < k < 3.625 \\ \Rightarrow k = -4,-3,-2,-1,0,1,2,3.\)
=> có 8 gợn lõm.

Đáp án: A
HD Giải:
Ta có: khoảng cách ngắn nhất giữa hai gợn lồi liên tiếp là 2cm → λ/2 = 2 → λ = 4cm
Hai nguồn ngược pha, nên điểm dao động với biên độ cực đại phải thỏa mãn: d2 – d1 = (k + 0,5)λ
Điểm dao động với biên độ cực tiểu thỏa mãn: d2 – d1 = k.λ
Số gợn lồi và lõm xuất hiện giữa hai điểm S1S2 là:
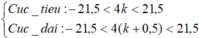
<=> 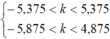
<=> 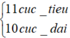

A,B là 2 nguồn cùng pha nên đường trung trực của AB dao động cực đại.
Giữa M và đường trung trực của AB có 3 dãy dực đại khác => M nằm trên dãy cực đại k = 4
\(d_2-d_1=(k+\frac{\triangle\varphi}{2\pi})\lambda = (4+0)\lambda \Rightarrow \lambda = \frac{d_2-d_1}{4}=\frac{21-19}{4}=0.5cm \Rightarrow v = f.\lambda = 80.0,5=40cm/s.\)
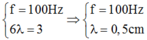
Đáp án A
Bước sóng chín
h bằng hai gơn lồi liên tiếp: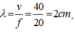 .
.
*Do tính chất đối xứng hai gợn lồi liên tiếp (tính từ cần rung) có đường kính chênh lệch nhau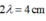 .
.