Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải
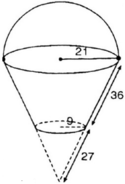
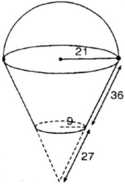
a) Diện tích cần tính gồm diện tích xung quanh của hình xung quanh của hình nón cụt và diện tích hình tròn đáy có bán kính 9cm.
Đường sinh của hình nón lớn là l = 36 + 27 = 63 cm.
Diện tích xung quanh của hình nón lớn, hình nón nhỏ:
S xq nón lớn = πrl = 3,14.21.63 =4154,22 (cm2)
S xq nón nhỏ = 3,14.9.27 =763,02 (cm2)
Diện tích xung quanh của hình nón cụt:
S xq nón cụt = S xq nón lớn -S xq nón nhỏ = 4154,22 - 763,02 = 3391,2 (cm2)
Diện tích hình tròn đáy:
Shình tròn đáy = 2 = 3,14.92 = 254,34 (cm2)
Diện tích mặt ngoài của xô:
S = S xq nón cụt + Shình tròn đáy = 3391,2 + 254,34 = 3645,54 (cm2)
b) Chiều cao của hình nón lớn:
h= = 59,397 (cm)
Chiều cao của hình nón nhỏ:
h' = = 25,546 (cm)
Thể tích của hình nón lớn:
Vhình tròn lớn = (1/3)πrh = (1/3). 3,14.212.59,397 = 27416,467 (cm3)
Thể tích hình nón nhỏ:
Vhình tròn nhỏ = (1/3)πrh = (1/3). 3,14.92.25,456 = 2158,160 (cm3)
Khi xô chứa đầy hóa chất thì dung tích của nó là:
V= Vhình tròn lớn -Vhình tròn nhỏ = 27416,467 - 2158,160 = 25258 (cm3)
= 25,3 (dm3)

a) a) Gọi l là đường sinh của hình nón lớn
Áp dụng định lý Ta – let ta có:
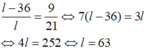
Vậy độ dài đường sinh của hình nón nhỏ là: 63 – 36 = 27
Diện tích xung quanh của hình nón lớn, hình nón nhỏ:


Chiều cao của hình nón lớn:
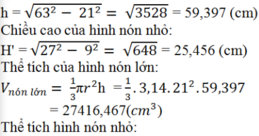
V n ó n n h ỏ = 1 3 π r 2 h = 1 3 . 3 , 14 . 9 2 . 25 , 456
= 2158,160 c m 3
Khi xô chứa đầy hóa chất thì dung dịch của nó là:
![]() = 27461,467 - 2158,160 = 25258
c
m
3
= 25,3
d
m
3
= 27461,467 - 2158,160 = 25258
c
m
3
= 25,3
d
m
3

Giải:
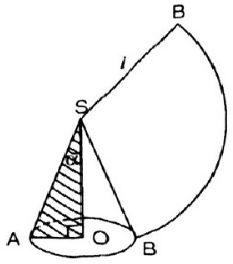
Diện tích hình quạt :
Diện tích xung quanh của hình nón: Sxq = π.r.l
Theo đầu bài ta có: Sxq= Sq => π.r.l=
Vậy l = 4r
Suy ra sin(a) = = 0,25
Vậy a = 14o28’

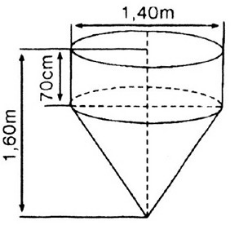
Giải: a) Thể tích cần tính gồm một hình trụ, đường kính đáy 1,4m, chiều cao 70cm, và một hình nón, bán kính đáy bằng bán kính hình trụ, chiều cao hình nón bằng 0,9m.
Thể tích hình trụ: Vtrụ = πR2h = 3,14. . 0.7 ≈ 1,077 (m3)
Thể tích hình nón: Vnón = (1/3). 3,14. .0,9 = 0,462 (m3)
Vậy thể tích cái phễu:
V = Vtrụ + Vnón = 1,077 + 0,462 = 1,539 (m3)
b) Diện tích cần tính gồm diện tích xung quanh hình trụ và diện tích xung quanh hình nón. Đường sinh của hình nón là:
Sxq trụ = 2πrh = 2.3,14.. 0,7= 3,077 (m2)
S xq nón = πrl = 3,14..1,4 = 2,506 (m2)
Vậy diện tích toàn phần của phễu:
S= Sxq trụ + S xq nón = 3,077 + 2,506 = 5,583 (m2)

Tham khảo
a, V = 9706 π cm 3 ≈9,71
b, S = π (81+23√554) ≈622,36

Gọi hình chữ nhật ban đầu là ABCDABCD có các cạnh AB=30cm,BC=20cmAB=30cm,BC=20cm.
Sau khi bớt mỗi cạnh của hình chữ nhật đi x(cm)x(cm), ta được hình chữ nhật mới là A′B′C′DA′B′C′D có các cạnh
A′B′=30−x(cm)A′B′=30−x(cm)
B′C′=20−x(cm)B′C′=20−x(cm)
Với yy là chu vi của hình chữ nhật A'B'C'D, ta có: y=2[(30−x)+(20−x)]y=2[(30−x)+(20−x)]
Rút gọn được y=−4x+100y=−4x+100.
Gọi hình chữ nhật ban đầu là ABCDABCD có các cạnh AB=30 cm, BC=20 cmAB=30cm,BC=20cm.
Sau khi bớt mỗi cạnh của hình chữ nhật đi x(cm)x(cm), ta được hình chữ nhật mới là A^{\prime} B^{\prime} C^{\prime} DA′B′C′D có các cạnh
A^{\prime} B^{\prime}=30-x(cm)A′B′=30−x(cm)
B^{\prime} C^{\prime}=20-x(cm)B′C′=20−x(cm)
Với yy là chu vi của hình chữ nhật A'B'C'D, ta có: y=2[(30-x)+(20-x)]y=2[(30−x)+(20−x)]
Rút gọn được y=-4 x+100y=−4x+100.

Áp dụng BĐT sau:\(2\left(a^2+b^2\right)\ge\left(a+b\right)^2\) ( dùng BĐT Bunhiacopski mà chứng minh :D )
Ta có:\(\frac{a+b}{a^2+b^2}=\frac{41}{9}\Rightarrow\frac{a^2+b^2}{a+b}=\frac{41}{9}\)
\(\Rightarrow\frac{82}{9}=\frac{2\left(a^2+b^2\right)}{a+b}\ge\frac{\left(a+b\right)^2}{a+b}=a+b\)
\(\Rightarrow a+b\le9\)
Mặt khác:\(41\left(a+b\right)=9\left(a^2+b^2\right);\left(41;9\right)=1\Rightarrow a+b⋮9\Rightarrow a+b=9\)
\(\Rightarrow a^2+b^2=41\)
Ta có hệ:\(\hept{\begin{cases}a+b=9\\a^2+b^2=41\end{cases}}\) giải cái hệ này là ra a,b nha < 3
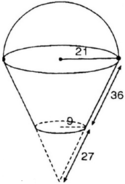
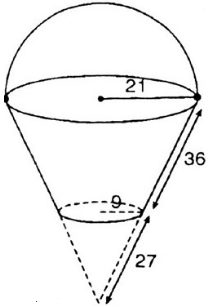
Gọi l là đường sinh của hình nón lớn
Áp dụng định lý Ta – let ta có:
Vậy độ dài đường sinh của hình nón nhỏ là: 63 – 36 = 27
Diện tích xung quanh của hình nón lớn, hình nón nhỏ:
S x q n ó n l ớ n = π r l = 3 , 14 . 21 . 63 = 454 , 22 c m 2
S x q n ó n n h ỏ = 3 , 14 . 9 . 27 = 763 , 02 c m 2
Diện tích xung quanh của xô là:
= 4154,22 - 763,02 = 3391,2 c m 2