Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta thấy cổng có hình bán nguyệt và chiều cao của cổng bằng một nửa chiều rộng của đường nên nó có dạng nửa đường tròn
Gắn trục tọa độ tại tim đường, ta có phương trình mô phỏng cái cổng là : \({x^2} + {y^2} = 4,{2^2}\) (với điều kiện \(y > 0\) vì cổng luôn nằm trên mặt đường)
b) Vì xe đi đúng làn nên ta có \(x = 2,2;y = 2,6\)
Khoảng cách từ điểm xa nhất của chiếc xe tài tới tim đường là: \(\sqrt {2,{2^2} + 2,{6^2}} \simeq 3,41\)
Ta thấy rằng \(3,41 < 4,2\), nên chiếc xe có thể đi qua cổng mà không làm hư hỏng cổng


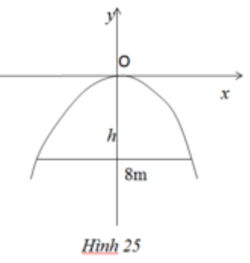
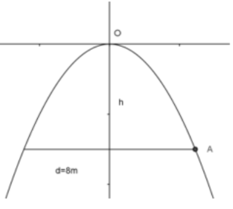
Vẽ lại parabol và chọn hệ trục tọa độ như hình dưới
Gọi phương trình của parabol là \({y^2} = 2px\)
Ta có chiều cao của cổng \(OH = BK = 10\), chiều rộng tại chân cổng \(BD = 2BH = 5\)
Vậy điểm B có tọa độ là \(B\left( {10;\frac{5}{2}} \right)\)
Thay tọa độ điểm B vào phương trình parabol ta có:
\({\left( {\frac{5}{2}} \right)^2} = 2p.10 \Rightarrow p = \frac{5}{{16}}\), suy ra phương trình parabol có dạng \({y^2} = \frac{5}{8}x\)
Thay \(x = 2\) vào phương trình \({y^2} = \frac{5}{8}x\) ta tìm được \(y = \frac{{\sqrt 5 }}{2}\)
Vậy bề rộng của cổng tại chỗ cách đỉnh 2 m là \(\sqrt 5 \) m

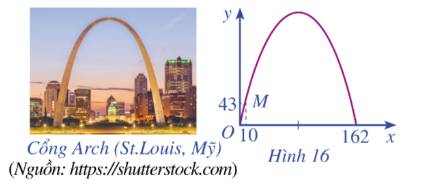
Từ đồ thị ta thấy các điểm thuộc đồ thị là: \(A\left( {0;0} \right),B\left( {10;43} \right),C\left( {162;0} \right)\).
Gọi hàm số là \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\)
Thay tọa độ các điểm A, B, C vào ta được hệ:
\(\left\{ \begin{array}{l}a{.0^2} + b.0 + c = 0\\a{.10^2} + b.10 + c = 43\\a{.162^2} + b.162 + c = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}c = 0\\100a + 10b = 43\\{162^2}a + 162b = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}c = 0\\a = - \frac{{43}}{{1520}}\\b = \frac{{3483}}{{760}}\end{array} \right.\)
Từ đố ta có \(y = - \frac{{43}}{{1520}}{x^2} + \frac{{3483}}{{760}}x\)
Hoành độ đỉnh của đồ thị là: \(x = - \frac{b}{{2a}} = 81\)
Khi đó: \(y = - \frac{{43}}{{1520}}{.81^2} + \frac{{3483}}{{760}}.81 \approx 186\)(m)
Vậy chiều cao của cổng là 186m.



a. Giả sử cái cổng hình bán nguyệt có dạng như hình vẽ
Cái cổng là nửa hình tròn có bán kính \(R=3,4m\)
Phương trình mô phỏng cái cổng là phương trình đường tròn tâm \(O\left(0;0\right)\)bán kính \(R=3,4m\) có dạng: \(x^2+y^2=11,56\)
b. Chiếc xe tải rộng \(2,4m\); cao \(2,5m\) ta có toạ độ điểm xa nhất của xe tải so với tâm của cổng là điểm \(M\left(2,4;2,5\right)\)
Ta có độ dài đoạn: \(OM=\left|\overrightarrow{OM}\right|\) mà \(\overrightarrow{OM}\left(2,4;2,5\right)\)
Vậy: \(\left|\overrightarrow{OM}\right|=\sqrt{2,4^2+2,5^2}\approx3,5\) suy ra độ dài đoạn thẳng \(OM=3,5m>R\)
Vì điểm xa nhất của xe tải lớn hơn bán kính đường tròn khi đi đúng làn đường xe tải không qua được cổng.