Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Diện tích một phần tư hình tròn là: \(\frac{1}{4}\pi {r^2}\)
Gọi x là biến số thể hiện kích thước của bán kính.
Công thức hàm số tính diện tích bồn hoa là: \(f(x) = \frac{1}{4}\pi {x^2}\)
+) Vì bán kính bồn hoa có kích thước từ 0,5 m đến 3 m nên \(0,5 \le x \le 3\)
Vậy tập xác định của hàm số này là \(D = [0,5;3]\)
b) Diện tích là \(0,5\pi \;{m^2}\) tức là\(f(x) = 0,5\pi \;\)
\( \Leftrightarrow \frac{1}{4}\pi {x^2} = 0,5\pi \Leftrightarrow {x^2} = 2 \Rightarrow x = \sqrt 2 \) (do \(0,5 \le x \le 3\))
Vậy bán kính bồn hoa bằng \(\sqrt 2 \;m\).
a) Vì công thức chu vi đường tròn là \(2\pi R\) với R là độ dài bán kính, trong đó \(\pi \) là số không thể tính chính xác được mà chỉ có thể lấy số gần đúng nên hai giá trị tính được là số gần đúng.
b)
Kết quả của An: \({S_1} = 2\pi R \approx 2.3,14.2 = 12,56\) cm:
Kết quả của Bình: \({S_2} = 2\pi R \approx 2.3,1.2 = 12,4\)cm.
Ta thấy \(\pi > 3,14 > 3,1 => 2.\pi. R > {S_1} > {S_2}\)
\( = > \left| {2\pi R - {S_1}} \right| < \left| {2\pi R - {S_2}} \right|\)
Nói cách khác, sai số tuyệt đối của \(S_1\) nhỏ hơn \(S_2\).
=> Kết quả của An chính xác hơn.
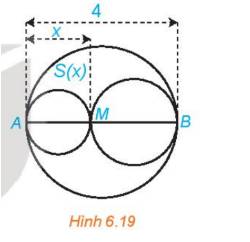
Ta có: AM<AB nên \(0 < x < 4\)
Diện tích hình tròn đường kính AB là \({S_0} = \pi .{\left( {\frac{{AB}}{2}} \right)^2} = 4\pi \)
Diện tích hình tròn đường kính AM là \({S_1} = \pi .{\left( {\frac{{AM}}{2}} \right)^2} = \frac{{\pi .{x^2}}}{4}\)
Diện tích hình tròn đường kính MB là \({S_2} = \pi .{\left( {\frac{{MB}}{2}} \right)^2} = \pi .\frac{{{{\left( {4 - x} \right)}^2}}}{4}\)
Diện tích phần hình phẳng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ là \(S(x) = {S_0} - {S_1} - {S_2} = 4\pi - \frac{{{x^2}}}{4}\pi - \frac{{{{\left( {4 - x} \right)}^2}}}{4}\pi = \frac{{ - {x^2} + 4x}}{2}\pi \)
Vì diện tich S(x) không vượt quá 1 nửa tổng diện tích hai hình tròn nhỏ nên:
\(S(x) \le \frac{1}{2}\left( {{S_1} + {S_2}} \right)\)
Khi đó : \(\frac{{ - {x^2} + 4x}}{2}\pi \le \frac{1}{2}.\frac{{{x^2} - 4x + 8}}{2}\pi \)
\( \Leftrightarrow - {x^2} + 4x \le \frac{{{x^2} - 4x + 8}}{2}\)
\( \Leftrightarrow - 2{x^2} + 8x \le {x^2} - 4x + 8\)
\( \Leftrightarrow 3{x^2} - 12x + 8 \ge 0\)
Xét tam thức \(3{x^2} - 12x + 8\) có \(\Delta ' = 12 > 0\) nên f(x) có 2 nghiệm phân biệt \({x_1} = \frac{{6 - 2\sqrt 3 }}{3};{x_2} = \frac{{6 + 2\sqrt 3 }}{3}\)
Mặt khác a=3>0, do đó ta có bảng xét dấu:
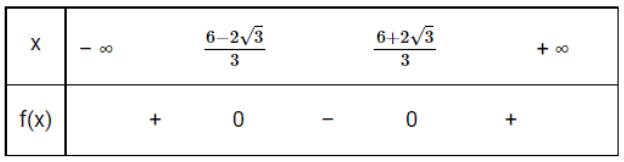
Do đó \(f(x) \ge 0\) với mọi \(x \in \left( { - \infty ;\frac{{6 - 2\sqrt 3 }}{3}} \right] \cup \left[ {\frac{{6 + 2\sqrt 3 }}{3}; + \infty } \right)\)
Mà 0<x<4 nên \(x \in \left( { - \infty ;\frac{{6 - 2\sqrt 3 }}{3}} \right] \cup \left[ {\frac{{6 + 2\sqrt 3 }}{3}; + \infty } \right)\)
a.Ta có : \(x\in\left(\pi;\dfrac{3}{2}\pi\right)\Rightarrow cosx< 0\)
\(cosx=-\sqrt{1-sin^2x}=-\sqrt{1-0,8^2}=-0,6\)
\(tanx=\dfrac{4}{3};cotx=\dfrac{3}{4}\)
b. cos 2x = \(cos^2x-sin^2x=0,6^2-0,8^2=-0,28\)
\(P=2.cos2x=-0,56\)
\(Q=tan\left(2x+\dfrac{\pi}{3}\right)=\dfrac{tan2x+tan\dfrac{\pi}{3}}{1-tan2x.tan\dfrac{\pi}{3}}=\dfrac{tan2x+\sqrt{3}}{1-tan2x.\sqrt{3}}\)
tan 2x = \(\dfrac{2tanx}{1-tan^2x}=\dfrac{\dfrac{2.4}{3}}{1-\left(\dfrac{4}{3}\right)^2}=\dfrac{-24}{7}\)
\(Q=\dfrac{-\dfrac{24}{7}+\sqrt{3}}{1+\dfrac{24}{7}.\sqrt{3}}\) \(=\dfrac{-24+7\sqrt{3}}{7+24\sqrt{3}}\)
Áp dụng định lý sin cho tam giác ABC, ta có:
\(2R_{giếng}=\dfrac{BC}{\sin A}=\dfrac{5}{\sin145^o}\) \(\Rightarrow R_{giếng}=\dfrac{5}{2\sin145^o}\) (m)
\(\Rightarrow S_{giếng}=\pi R_{giếng}^2=\pi\left(\dfrac{5}{2\sin145^o}\right)^2\approx59,68\left(m^2\right)\)
Chu vi đường tròn là:
\(P = 2\pi R = 2\pi .1 = 2\pi \left( {cm} \right)\)
Bấm máy tính ta thấy \(2\pi \approx 6,28\)
Vậy \(P \approx 6,28cm\).
Chú ý
Ta có thể lấy số gần đúng khác của \(2\pi \) như: 6,283 hoặc 6,283185
Để phương trình x 2 + y 2 + m − 4 x + m + 2 y + 3 m + 10 = là phương trình của một đường tròn có bán kính R = 2 thì:
m − 4 2 2 + m + 2 2 2 − ( 3 m + 10 ) = 2 2 = 4 ⇔ m 2 − 8 m + 16 4 + m 2 + 4 m + 4 4 − 3 m − 10 − 4 = 0 ⇔ 2 m 2 − 4 m + 20 4 − 3 m − 14 = 0
⇔ 2 m 2 − 4 m + 20 − 12 m − 56 = 0 ⇔ 2 m 2 − 16 m − 36 = 0 ⇔ m = 4 ± 34
ĐÁP ÁN A
a) Công thức tính diện tích S của bồn hoa là: \(S = \pi .{R^2} = \pi .0,{8^2}\left( {{m^2}} \right)\)
b) Giá trị \(\left| {S - 1,984} \right|\) biểu diễn độ lệch giữa số “1,984” và S.