Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi độ cao của một lỗ thủng trên thành bình là h. Theo công thức Toorrixenli, vận tốc của tia nước khi vừa mới phun ra khỏi lỗ là: v 0 = 2 g ( H − h ) .
Xét chuyển động của một giọt nước khi vừa bắn ra khỏi lỗ cho đến lúc va chạm bàn.
Theo định luật bảo toàn cơ năng, ta có: m g h + 1 2 m v 0 2 = 1 2 m v 2
⇒ m g h + 1 2 m 2 g ( H − h ) = 1 2 m v 2 hay m g H = 1 2 m v 2
Vận tốc của nước khi vừa chạm bàn: v = 2 g H .
Giá trị này không phụ thuộc h, nghĩa là mọi tia nước khi rơi chạm bàn đều có cùng một độ lớn vận tốc.

Đáp án: A
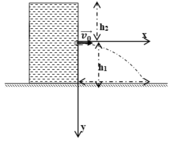
- Tại thời điểm mặt thoáng của nước cách lổ khoảng h2, vận tốc phần tử nước ở mặt thoáng bằng không, vận tốc phần tử nước ở lỗ là v0, ta có
![]()
- Khi nước chảy ra khỏi lỗ, các giọt nước chuyển động như vật chuyển động ném ngang với các phương trình chuyển động:
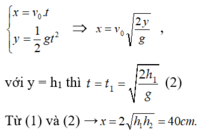

1/ Đáp án B
2/
a) Thời gian vật rơi:
\(t=\frac{v}{g}=3\left(s\right)\)
- Độ cao thả vật:
\(h=\frac{1}{2}gt^2=45\left(m\right)\)
b) Quãng đường vật rơi trong giây cuối cùng trước khi chạm đất :
\(\Delta s'=s_3-s_2=25\left(m\right)\)
1.B
2. a) h=\(\dfrac{v^2}{2g}\)=\(\dfrac{30^2}{2.10}\)=45(m)
t=\(\dfrac{v}{g}\)=\(\dfrac{30}{10}\)=3(s)
b) S2s=\(\dfrac{1}{2}\)gt2s2=\(\dfrac{1}{2}\).10.22=20(m)
\(\Delta S\)=S3s-S2s=h-S2s=25(m)

Bạn nhớ viết hoa đầu dòng nhé, và quy tắc bỏ dấu trong văn bản word:
Hướng dẫn:
Cơ năng ban đầu: W1 = mgh
Cơ năng khi chạm đất: W2 = 1/2 mv2
Bảo toàn cơ năng: \(W_1=W_2\Rightarrow v=\sqrt{2gh}\)

a)
Chọn chiều (+) hướng lên. Gốc thời gian lúc bắt đầu ném
\(y=v_0t+\frac{gt2}{2}=20t-5t^2\) (1)
\(v=v_0+gt=20-10t\) (2)
Tại điểm cao nhất v=0
Từ (2) \(\Rightarrow\) t=2(s) thay vào (1)
yM = 20(m)
b)
Khi chạm đất y=0 từ (1)\(\Rightarrow\) t=0 và t=4 (s)
Thay t = 4 (s) vào (2) \(v'=-20m\text{/}s\)
(Dấu trừ (-) vận tốc ngược với chiều dương.)

Ta xét chuyển động của viên bi B có vận tốc trước khi va chạm là vB=0m/s, sau va chạm viên bi B có vận tốc v=0,5m/s
Áp dụng biểu thức xác định gia tốc
a = v 2 − v 1 Δ t = 0 , 5 0 , 2 = 2 , 5 m / s 2
Theo định luật III Niu-tơn: F → A B = − F → B A
Theo định luật II, ta có: F=ma
→ | F A B | = | F B A | ↔ m A | a A | = m B a B → a A = m B | a B | m A = 0 , 6.2 , 5 0 , 3 = 5 m / s 2
Sử dụng biểu thức tính vận tốc theo a:
v=v0+at=3+5.0,2=4m/s
Đáp án: C

Chọn B.
Công thức tính độ lớn vận tốc v của vật ngay trước khi chạm đất của vật rơi tự do là:
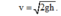
Đáp án: A
Gọi độ cao của một lỗ thủng trên thành bình là h.
Tại thời điểm mặt thoáng của nước cách lổ khoảng h1 = H - h, vận tốc phần tử nước ở mặt thoáng bằng không, vận tốc phần tử nước ở lỗ là v0, ta có:
(H là độ cao của bình nước)
Xét chuyển động của một giọt nước khi vừa bắn ra khỏi lỗ cho đến lúc va chạm bàn.
Theo định luật bảo toàn cơ năng, ta có:
Vận tốc của nước khi vừa chạm bàn: v = 2 g h
Giá trị này không phụ thuộc h, nghĩa là mọi tia nước khi rơi chạm bàn đều có cùng một độ lớn vận tốc.