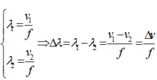Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Khi ánh sáng truyền từ môi trường này sang môi trường khác thì tần số không đổi, nhưng vì các môi trường có chiết suất khác nhau nên vận tốc truyền sáng khác nhau và dẫn đến bước sóng thay đổi.
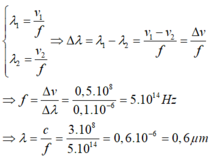

Phương pháp: Áp dụng công thức tính bước sóng
Cách giải:
Khi ánh sáng truyền từ môi trường này sang môi trường khác thì tần số không đổi, nhưng vì các môi trường có chiết suất khác nhau nên vận tốc truyền sáng khác nhau và dẫn đến bước sóng thay đổi.
Ta có:
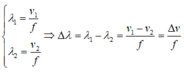
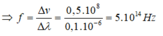
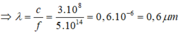
Đáp án C

1/ Các đáp án B, C, D chỉ đúng khi các điểm này nằm trên cùng một phương truyền sóng.
\(\rightarrow\) Chọn đáp án A
2/ Khi các sóng truyền từ không khí vào nước thì tần số sóng không đổi còn bước sóng thay đổi sao cho \(f=\frac{v}{\lambda}=\)const .Khi truyền từ không khí vào nước vận tốc của sóng âm tăng nên bước sóng sẽ tăng, vận tốc của sóng ánh sáng giảm nên bước sóng sẽ giảm.
\(\rightarrow\)Chọn đáp án B

Tịnh tiến màn quan sát lại gần mặt phẳng chưa hai khe 25 cm tức là \(D' = D-0,25.\)
\(i_1 = \frac{\lambda D}{a}\\
i_2 =\frac{\lambda (D-0,25)}{a} \)=> \(\frac{i}{i'}= \frac{D}{D-0,25}= \frac{5}{4}\)
=> \(D = 5.0,25 = 1,25m.\)
=> \(\lambda = \frac{i.a}{D}= 0,48 \mu m.\)
Chú ý là giữ nguyên đơn vị i (mm); a (mm) ; D (m) thì đơn vị bước sóng \(\lambda (\mu m)\).

Tại vị trí vân bậc 4 của bước sóng 0,76um còn có vân sáng khác \(\Rightarrow ki=k'i'\)
k = 4
\(\Rightarrow k.\lambda = k'\lambda'\)
\(\Rightarrow 4.0,76 = k'\lambda'\)
\(0,38\mu m \le\lambda<0,76\mu m\)
\(\Rightarrow 4< k \le 8\)
\(\Rightarrow k =5;6;7;8\)
Vậy có 4 vân sáng thỏa mãn.

\( i = \frac{\lambda D}{a}= 0,64 mm.\)
Số vân tối quan sát được trên màn là
\(N_t = 2.[\frac{L}{2i}+0,5]=2.9=18.\)



Đáp án C
Khi ánh sáng truyền từ môi trường này sang môi trường khác thì tần số không đổi, nhưng vì các môi trường có chiết suất khác nhau nên vận tốc truyền sáng khác nhau và dẫn đến bước sóng thay đổi.
Ta có: