K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HM
1
21 tháng 12 2021
\(\Leftrightarrow x^2-6x+9-x^2+4=1\)
=>-6x=-12
hay x=2
14 tháng 3 2022
Ta có:
(2 - 3x)(x + 8) = (3x - 2)(3 - 5x)
⇔ (2 - 3x)(x + 8) - (3x - 2)(3 - 5x) = 0
⇔ (2 - 3x)(x + 8) + (2 - 3x)(3 - 5x) = 0
⇔ (2 - 3x)(x + 8 + 3 - 5x) = 0
⇔ (2 - 3x)(11 - 4x) = 0
⇔ 2 - 3x = 0 hay 11 - 4x = 0
⇔ 2 = 3x hay 11 = 4x
⇔ x = \(\dfrac{2}{3}\) hay x = \(\dfrac{11}{4}\)
Vậy tập nghiệm của pt S = \(\left\{\dfrac{2}{3};\dfrac{11}{4}\right\}\)
14 tháng 3 2022
<=> (2-3x ) (x+8) + (2-3x ) (3-5x)=0
<=> (2-3x ) ( x+8 + 3-5x ) =0
<=> (2-3x ) ( 11 - 4x ) = 0
=> 2-3x =0 hoặc 11-4x =0
3x = 2 4x =11
x = 2/3 x = 11/4
16 tháng 12 2022
2x^2+y^2+9=6x+2xy
=>x^2+y^2+9-6x-2xy+x^2=0
=>(x-3)^2+(y-x)^2=0
=>x=y=3
=>A=3^4039-3^4039+1/9*3*3=1
MD
1
18 tháng 8 2021
Ta có: \(\left(3x-1\right)\left(2x+7\right)-\left(x+1\right)\left(6x-5\right)=\left(x+2\right)-\left(x-5\right)\)
\(\Leftrightarrow6x^2+21x-2x-7-6x^2+5x-6x+5=x+2-x+5\)
\(\Leftrightarrow18x-2=7\)
\(\Leftrightarrow18x=9\)
hay \(x=\dfrac{1}{2}\)
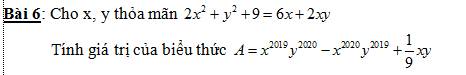
\(x^2-9x+20=0\)
\(\Leftrightarrow x^2-4x-5x+20=0\)
\(\Leftrightarrow x\left(x-4\right)-5\left(x-4\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(x-5\right)=0\)
\(\Rightarrow\hept{\begin{cases}x-4=0\\x-5=0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=4\\x=5\end{cases}}\)
Vậy tập nghiện của PT là S = { 4 ; 5 }
x2 - 9x + 20 = 0
<=> x2 - 4x - 5x + 20 = 0
<=> x( x - 4 ) - 5( x - 4 ) = 0
<=> ( x - 4 )( x - 5 ) = 0
<=> x - 4 = 0 hoặc x - 5 = 0
<=> x = 4 hoặc x = 5
Vậy phương trình có tập nghiệm S = { 4 ; 5 }