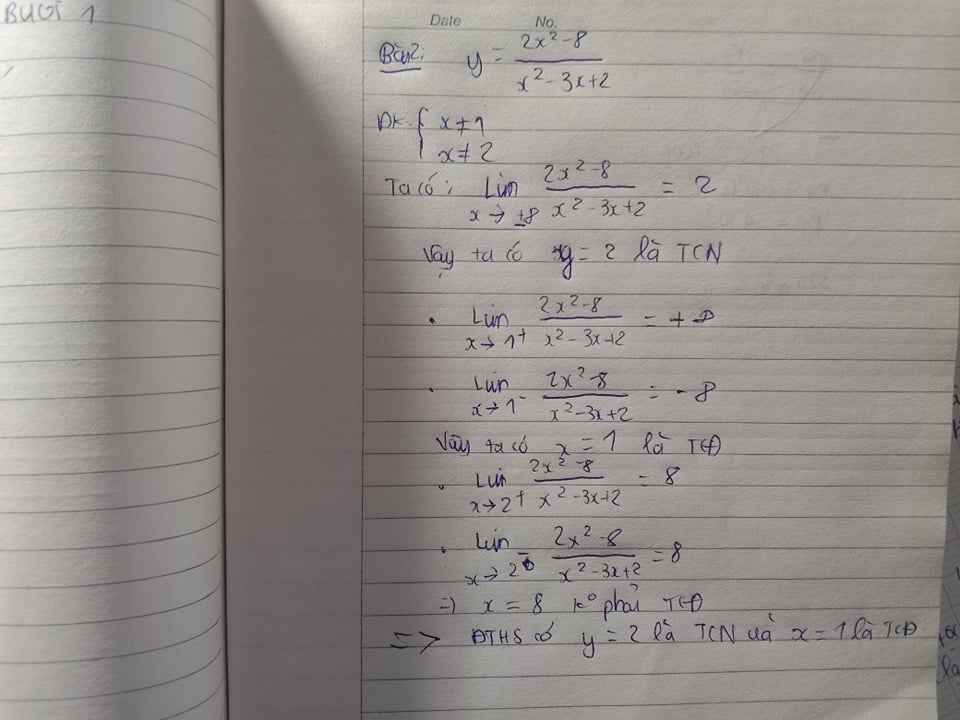Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


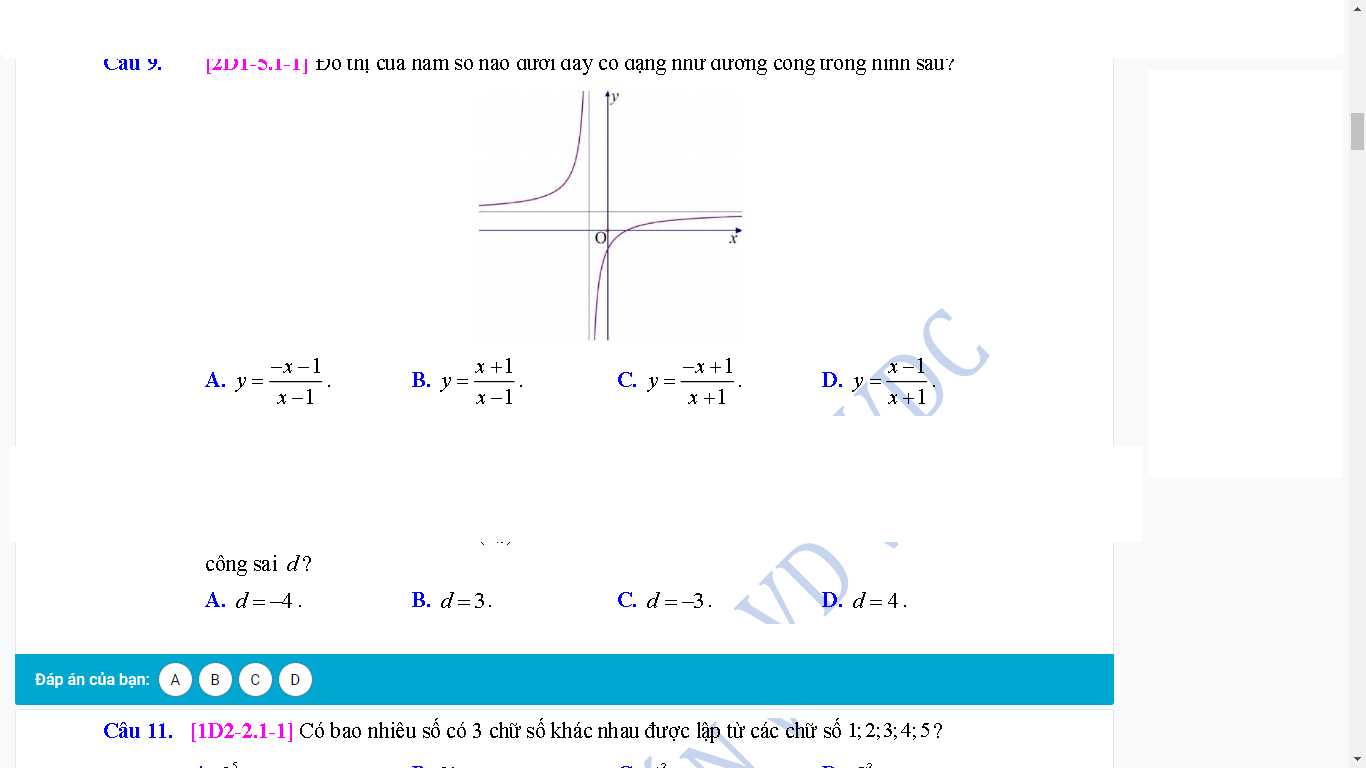
- Tiệm cận đứng của đồ thị là 1 giá trị âm nên loại A và B
- Hàm đồng biến trên các khoảng xác định nên loại C
Vậy D là đáp án đúng

\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên

a. Để hàm số đã cho có một cực trị thì -m(2m-1)>0 \(\Rightarrow\) 0<m<1/2.
b. Để hàm số đã cho có ba cực trị thì -m(2m-1)<0 \(\Rightarrow\) m<0 hoặc m>1/2.
c. Để hàm số đã cho có một cực trị là cực đại thì m<0 và -(2m-1)<0, suy ra không có giá trị nào của m thỏa yêu cầu của bài toán.


Mặt cầu tâm \(I\left(1;1;0\right)\) bán kính \(R=5\)
\(\Rightarrow IA=\sqrt{6^2+8^2}=10=2R\)
Gọi C là trung điểm IA \(\Rightarrow C\left(4;5;0\right)\Rightarrow IC=R=5\Rightarrow C\in\left(S\right)\)
Gọi D là trung điểm IC \(\Rightarrow D\left(\dfrac{5}{2};3;0\right)\), đồng thời do D là trung điểm IC \(\Rightarrow MD\perp IC\) và IM=IC=R hay tam giác MDF vuông tại D
Lại có: \(CM=CA=CI=R\Rightarrow\) tam giác AMI vuông tại M
\(\Rightarrow\Delta_VMID\sim\Delta_VAIM\) (chung góc I)
\(\Rightarrow\dfrac{MA}{MD}=\dfrac{AI}{AM}=\dfrac{2R}{R}=2\Rightarrow MA=2MD\)
\(\Rightarrow P=MA+2MB=2MD+2MB=2\left(MD+MB\right)\ge2DB=2\sqrt{\left(\dfrac{5}{2}\right)^2+\left(3-8\right)^2+0^2}=5\sqrt{5}\)

Bài 5:
\(y=m\sqrt{x^2-4x+7}-(3x-4)=\frac{(m^2-9)x^2+(24-4m^2)x+(7m^2-16)}{m\sqrt{x^2-4x+7}+3x-4}\)
Để đths $y$ có TCN thì:\(\lim\limits_{x\to \pm \infty}y\) hữu hạn
Để điều này xảy ra thì $m^2-9=0\Leftrightarrow m=\pm 3$
Kiểm tra lại thấy cả 2 giá trị này đều thỏa mãn.
Bài 6: Tiệm cận của ĐTHS chứ làm gì có tiệm cận hàm số hả bạn?
a.
\(y=\frac{x^2-3x+2}{2x^2+x-1}=\frac{x^2-3x+2}{(2x-1)(x+1)}\)
$(2x-1)(x+1)=0\Leftrightarrow x=\frac{1}{2}$ hoặc $x=-1$
Do đó TCĐ của ĐTHS là $x=\frac{1}{2}$ và $x=-1$
Mặt khác: \(\lim\limits_{x\to \pm \infty}\frac{x^2-3x+2}{2x^2+x-1}=\frac{1}{2}\) nên $y=\frac{1}{2}$ là TCN của ĐTHS.
b.
$x+1=0\Leftrightarrow x=-1$ nên $x=-1$ là TCĐ của đths
$\lim\limits_{x\to \pm \infty}\frac{1-x}{1+x}=-1$ nên $y=-1$ là TCN của đths

\(y'=3mx^2-4mx-\left(m+1\right)\)
- Với \(m=0\Rightarrow y'=-1< 0\) hàm nghịch biến trên R (thỏa)
- Với \(m\ne0\) hàm nghịch biến trên R khi:
\(\left\{{}\begin{matrix}3m< 0\\\Delta'=4m^2+3m\left(m+1\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\7m^2+3m\le0\\\end{matrix}\right.\)
\(\Leftrightarrow-\dfrac{3}{7}\le m< 0\)
Vậy \(-\dfrac{3}{7}\le m\le0\Rightarrow m=0\)
S có 1 phần tử