K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MT
1
22 tháng 10 2021
\(A=\dfrac{20^{10}+1}{20^{10}-1}=1-\dfrac{2}{20^{10}-1}\)
\(B=\dfrac{20^{10}-1}{20^{10}-3}=1-\dfrac{2}{20^{10}-3}\)
Do đó: A>B
BN
1
13 tháng 10 2021
a) \(\Rightarrow\left(x-3\right)\left(x+4\right)=5.12\)
\(\Rightarrow x^2+x-72=0\)
\(\Rightarrow\left(x-8\right)\left(x+9\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=8\\x=-9\end{matrix}\right.\)
b) \(\Rightarrow\left(x+3\right)^2=36\)
\(\Rightarrow\left[{}\begin{matrix}x+3=6\\x+3=-6\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=3\\x=-9\end{matrix}\right.\)
c) \(\Rightarrow2x^2=8\Rightarrow x^2=4\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
15 tháng 4 2022
a: Xét ΔAMB và ΔANC có
AM=AN
\(\widehat{BAM}\) chung
AB=AC
Do đó: ΔAMB=ΔANC
Xét ΔBNC và ΔCMB có
NB=MC
BC chung
NC=MB
Do đó: ΔBNC=ΔCMB
b: Ta có: ΔABM=ΔACN
nên BM=CN
Xét ΔGBC có \(\widehat{GBC}=\widehat{GCB}\)
nên ΔGBC cân tại G
Xét ΔABG và ΔACG có
AB=AC
BG=CG
AG chung
Do đó: ΔABG=ΔACG
Suy ra: \(\widehat{BAG}=\widehat{CAG}\)
hay AG là tia phân giác của góc BAC
HN
2
26 tháng 8 2021
a: Xét ΔABD và ΔHBD có
BA=BH
\(\widehat{ABD}=\widehat{HBD}\)
BD chung
Do đó: ΔABD=ΔHBD
b: Ta có: ΔABD=ΔHBD
nên \(\widehat{BAD}=\widehat{BHD}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BHD}=90^0\)
hay DH\(\perp\)BC
13 tháng 10 2021
đúng rồi ạ, giúp em với ạ hoặc làm đc câu nào giúp em cũng được ạ
NT
4
28 tháng 10 2019
Câu hỏi của TRẦN THỊ BÍCH HỒNG - Toán lớp 7 - Học toán với OnlineMath
MD
2
2 tháng 3 2016
\(\frac{4x}{6y}=\frac{2x+8}{3y+11}\Leftrightarrow\frac{2x}{3y}=\frac{2x+8}{3y+11}\Rightarrow2x\left(3y+11\right)=3y\left(2x+8\right)\Leftrightarrow6xy+11x=6yx+24y\)
\(\Leftrightarrow11x=24y\Leftrightarrow\frac{x}{y}=\frac{24}{11}\)
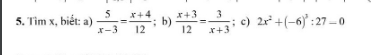
Bạn tự vẽ hình nhé
Giải
a, Xét \(\Delta\)BAD và \(\Delta CAD\), có :
AB = AC ( \(\Delta ABC\) cân tại A )
góc BAD = góc CAD ( AD là tpg góc BAC )
AD : cạnh chung
\(\Rightarrow\Delta BAD=\Delta CAD\)( c-g-c )
b, Ta có : \(\Delta ABC\) cân tại A ( gt ), mà AD là đường phân giác của \(\Delta ABC\) ( gt )
\(\Rightarrow\)AD đồng thời là đường trung tuyến \(\Delta ABC\) ( t/c \(\Delta\) cân )
Mà AD cắt BE tại G ( gt ) \(\Rightarrow\) G là trọng tâm \(\Delta\) ABC ( đ/n )
\(\Rightarrow\)GB = 2 GE ( t/c )
Ta có AB = AC ( cmt ) \(\Rightarrow\)2 đường trung tuyến của 2 đoạn thẳng này cũng bằng nhau
\(\Rightarrow\)Đường trung tuyến của AB = BE \(\Rightarrow\) CG = BG = 2. GE \(\Rightarrow\) CG = 2 GE
Mình làm trước 2 câu này, máy hết pin rồi.