Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y'=8x^3-8x\)
a. Đường thẳng \(x-48y+1=0\) có hệ số góc \(\dfrac{1}{48}\) nên tiếp tuyến có hệ số góc \(k=-48\)
\(\Rightarrow8x^3-8x=-48\Rightarrow x^3-x+6=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2-2x+3\right)=0\Rightarrow x=-2\)
\(y'\left(-2\right)=47\)
Phương trình tiếp tuyến: \(y=-48\left(x+2\right)+47\)
b. Gọi tiếp điểm có hoành độ \(x_0\)
Phương trình tiếp tuyến: \(y=\left(8x_0^3-8x_0\right)\left(x-x_0\right)+2x^4_0-4x^2_0-1\) (1)
Do tiếp tuyến qua A:
\(\Rightarrow-3=\left(8x_0^3-8x_0\right)\left(1-x_0\right)+2x_0^4-4x^2_0-1\)
\(\Leftrightarrow3x_0^4-4x_0^3-2x_0^2+4x_0-1=0\)
\(\Leftrightarrow\left(x_0-1\right)^2\left(3x_0^2+2x_0-1\right)=0\Rightarrow\left[{}\begin{matrix}x_0=1\\x_0=-1\\x_0=\dfrac{1}{3}\end{matrix}\right.\)
Có 3 tiếp tuyến thỏa mãn. Thay lần lượt các giá trị \(x_0\) bên trên vào (1) là được

Chọn D.
Gọi M(xo; yo) là tiếp điểm của của tiếp tuyến và đồ thị hàm số.
f'(x) = x02 + xo – 2.
Viết lại d: y = 4x + 2 ⇒ Hệ số góc k = 4
Vì tiếp tuyến cần tìm song song với d nên: 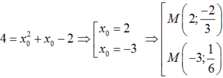
Với  , pttt là:
, pttt là: 
Với  , pttt là:
, pttt là: 
KL:Có hai tiếp tuyến thỏa mãn ycbt là ![]() và
và  .
.

f ' = 6x2 - 8x
a. f '(x) < 0
<=> 6x2 - 8x < 0
<=> 0 < x < \(\dfrac{4}{3}\)
b. do tt ss với đt y = 5 - 2x
nên tt có hsg k = -2
ta có y' = 6x2- 8x = -2
=> \(\left[{}\begin{matrix}x=1\\x=\dfrac{1}{3}\end{matrix}\right.\)
với x = 1 => y = 1
vập pttt: y = -2( x - 1) + 1
<=> y = -2x + 3
với x = \(\dfrac{1}{3}\) => y = \(\dfrac{23}{9}\)
vập pttt y= -2 (x-\(\dfrac{1}{3}\)) +\(\dfrac{23}{9}\)
<=> y= -2x +\(\dfrac{29}{9}\)

\(AB=\sqrt{\left(-5-3\right)^2+\left(3-1\right)^2}=2\sqrt{17}\)
\(\Rightarrow R=\frac{AB}{2}=\sqrt{17}\)
Gọi I là tâm đường tròn \(\Rightarrow\) I là trung điểm AB \(\Rightarrow I\left(-1;2\right)\)
Phương trình đường tròn: \(\left(x+1\right)^2+\left(y-2\right)^2=17\)
b/ Đường tròn tâm \(I\left(-2;1\right)\) bán kính \(R=4\)
Do tiếp tuyến song song với d nên pt tiếp tuyến d' có dạng \(4x-3y+c=0\)
Do d' là tiếp tuyến nên \(d\left(I;d'\right)=R\)
\(\Rightarrow\frac{\left|-2.4-3.1+c\right|}{\sqrt{4^2+\left(-3\right)^2}}=4\Leftrightarrow\left|c-11\right|=20\Rightarrow\left[{}\begin{matrix}c=31\\c=-9\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}4x-3y+31=0\\4x-3y-9=0\end{matrix}\right.\)

a: \(f'\left(x\right)=\dfrac{\left(2x+2\right)'\cdot\left(x-1\right)-\left(2x+2\right)\cdot\left(x-1\right)'}{\left(x-1\right)^2}\)
\(=\dfrac{2\left(x-1\right)-2x-2}{\left(x-1\right)^2}=\dfrac{-4}{\left(x-1\right)^2}\)
y-y0=f'(x0)*(x-x0)
=>y=y0+f'(x0)*(x-x0)=f(x0)+f'(x0)(x-x0)
(d)//-4x+8 nên f(x0)=-4
=>2x+2=-4x+4
=>6x=2
=>x=1/3
f'(1/3)=-4/(1/3-1)^2=-9
y=-4+(-9)(x-1/3)=-4-9x+3=-9x-1
b: (d) vuông góc y=4x+3
=>(d): y=-1/4x+b
(d): y=f(x0)+f'(x0)*(x-x0)
=>f(x0)=-1/4
=>2x+2=-1/4(x-1)=-1/4x+1/4
=>9/4x=-7/4
=>x=-7/9
f'(-7/9)=-4/(-7/9-1)^2=-81/64
y=f(-7/9)+f'(-7/9)*(x+7/9)
=-1/4-81/64(x+7/9)
=-81/64x-79/64

Gọi `M(x,y)` là điểm thuộc TT.
`y'=3x^2+2x`
TT song song với `y=8x+9=> f'(x_0)=8`
`=> 3x_0^2+2x_0=8`
`<=>` \(\left[{}\begin{matrix}x_0=\dfrac{4}{3}\\x_0=-2\end{matrix}\right.\)
TH1: `x_0=4/3 => y_0 = 193/27`
`=>` PTTT: `y=8(x-4/3)+193/27=8x-96/27`
TH2: `x_0=-2 => y_0=-1`
`=>` PTTT: `y=8(x+2)-1=8x+15`
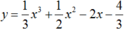 .
.
Chắc đề yêu cầu viết pt tiếp tuyến?
\(y=\frac{x+3}{x-1}\Rightarrow y'=\frac{-4}{\left(x-1\right)^2}\)
a/ Do tiếp tuyến song song với \(x+y+2=0\Leftrightarrow y=-x-2\) nên có hệ số góc bằng -1
\(\Rightarrow\frac{-4}{\left(x_0-1\right)^2}=-1\Rightarrow\left(x_0-1\right)^2=4\Rightarrow\left[{}\begin{matrix}x_0=5\Rightarrow y_0=2\\x_0=-3\Rightarrow y_0=0\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=-1\left(x-5\right)+2\\y=-1\left(x+3\right)+0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}y=-x+7\\y=-x-3\end{matrix}\right.\)
b/ \(4x-y+1=0\Leftrightarrow y=4x+1\)
Do tiếp tuyến vuông góc với d' nên
\(-\frac{4}{\left(x_0-1\right)^2}.\left(4\right)=-1\Leftrightarrow\left(x_0-1\right)^2=16\Rightarrow\left[{}\begin{matrix}x_0=17\Rightarrow y_0=\frac{5}{4}\\x_0=-15\Rightarrow y_0=\frac{3}{4}\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=-\frac{1}{4}\left(x-17\right)+\frac{5}{4}\\y=-\frac{1}{4}\left(x+15\right)+\frac{3}{4}\end{matrix}\right.\)
Bạn tự rút gọn nhé