Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 4 :
\(M=\left(2x-3y\right)^2-\left(3y-2\right)\left(3y+2\right)-\left(1-2x\right)^2+4x\left(3y-1\right)\)
\(=\left(2x-3y-1+2x\right)\left(2x-3y+1-2x\right)-9y^2+4+12xy-4x\)
\(=\left(4x-3y-1\right)\left(1-3y\right)-9y^2+4+12xy-4x\)
\(=4x-12xy-3y+9y^2-1+3y-9y^2+4+12xy-4x=3\)
Vậy biểu thức ko phụ thuộc giá trị biến x
Bài 2 :
a, \(\left(a-3b\right)^2=a^2-6ab+9b^2\)
b, \(x^2-16y^4=\left(x-4y^2\right)\left(x+4y^2\right)\)
c, \(25a^2-\frac{1}{4}b^2=\left(5a-\frac{1}{2}b\right)\left(5a+\frac{1}{2}b\right)\)
Bài 3 :
a, \(9x^2-6x+1=\left(3x-1\right)^2\)
b, \(\left(2x+3y\right)^2+2\left(2x+3y\right)+1=\left(2x+3y+1\right)^2\)
c, \(4\left(2x-y\right)^2-8x+4y+1=\left(4x-2y\right)^2-2\left(4x-2y\right)+1=\left(4x-2y-1\right)^2\)

Bài giải:
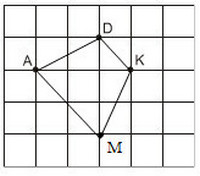
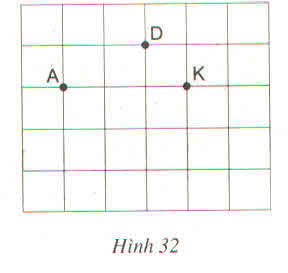
Có thể tìm được hai điểm M là giao điểm của các dòng kẻ sao cho nó cùng với ba điểm đã cho A, D, K là bốn đỉnh của một hình thang cân. Đó là hình thang AKDM1 (với AK là đáy) và hình thang ADKM2 (với DK là đáy).
 mọi người giải hộ em ạ , em cảm ơn nhiều . Phần kia G
mọi người giải hộ em ạ , em cảm ơn nhiều . Phần kia G



 Mọi Người giải giúp em ạ em cảm ơn ạ
Mọi Người giải giúp em ạ em cảm ơn ạ 

 mọi người giải giúp em với ạ em đang cần gấp lắm ạ
mọi người giải giúp em với ạ em đang cần gấp lắm ạ 




a: Xét ΔBAC vuông tại A và ΔBHA vuông tại H có
góc B chung
=>ΔBAC đồng dạng với ΔBHA
=>BA/BH=BC/BA
=>BA^2=BH*BC
b: BA^2=BH*BC
=>BM^2=BH*BC
=>BM/BH=BC/BM
=>ΔBMC đồng dạng với ΔBHM
=>góc BMH=góc BCM