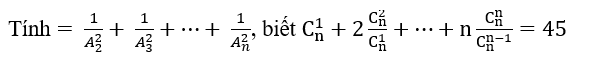Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phần bên trên giải thích rồi còn gì
n + n - 1 + n - 2 + n - 3 + .... + 1
Tổng của dãy số hơn kém 1 đơn vị lùi từ n về 1
T = (Số đầu - số cuối) . số số hạng rồi chia 2
tức là \(\dfrac{\left(n-1\right).n}{2}\)

Đáp án C
Gieo 2 lần ta có 36 kết quả, trong đó có 18 trường hợp ra tổng 2 lần chẵn, 18 trường hợp ra lẻ.
Đến lần gieo thứ 3, ta có
+) Nếu tổng 2 lần trước là chẵn, lần 3 là chẵn thì tổng 3 lần chẵn, suy ra có 3 kết quả
+) Nếu tổng 2 lần trước là lẻ, lần 3 là lẻ thì tổng 3 lần chẵn, suy ra có 3 kết quả
Với 18 lần chẵn và 18 lần được lẻ trong 2 lần gieo trước, số các kết quả thỏa mãn là 18.3 + 18.3 = 108.

Đầu tiên cần phải định nghĩa rõ ràng "theo thứ tự" ở đây nghĩa là gì?
Theo thứ tự nếu mang nghĩa 12345 khác 54321 (thứ tự phải qua trái khác trái qua phải) thì xác suất là \(\dfrac{1}{120}\)
Còn "theo thứ tự" mang nghĩa 12345 cũng giống 54321 (thứ tự chiều trái phải như nhau) thì xác suất mới là \(\dfrac{1}{60}\)

\(\Leftrightarrow2cos^2x-1-\left(2m-3\right)cosx+m-1=0\)
\(\Leftrightarrow2cos^2x-\left(2m-3\right)cosx+m-2=0\)
\(\Leftrightarrow\left(2cosx-1\right)\left(cosx-m+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=\dfrac{1}{2}\\cosx=m-2\end{matrix}\right.\)
Do \(cosx=\dfrac{1}{2}\Rightarrow x=\dfrac{\pi}{3}+k2\pi\) ko có nghiệm thuộc khoảng đã chi
\(\Rightarrow cosx=m-2\) có nghiệm thuộc \(\left(\dfrac{\pi}{2};\dfrac{3\pi}{2}\right)\)
Ta có \(x\in\left(\dfrac{\pi}{2};\dfrac{3\pi}{2}\right)\Rightarrow cosx\in\left(-1;0\right)\)
\(\Rightarrow-1< m-2< 0\)
\(\Rightarrow1< m< 2\)

a)
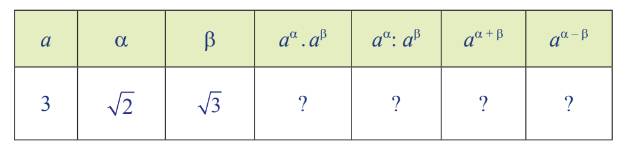
| a | α | b | \(a^{\alpha}\cdot a^{\beta}\) | \(a^{\alpha}:a^{\beta}\) | \(a^{\alpha+\beta}\) | \(\alpha^{\alpha+\beta}\) |
| 3 | \(\sqrt{2}\) | \(\sqrt{3}\) | \(3^{\sqrt{2}}\cdot3^{\sqrt{3}}=31,70659\) | \(3^{\sqrt{2}}:3^{\sqrt{3}}=0,70527\) | \(3^{\sqrt{2}+\sqrt{3}}=31,70659\) | \(3^{\sqrt{2}-\sqrt{3}}=0,70527\) |
b) Nhận xét:
\(a^m\cdot a^n=a^{m+n};a^m:a^n=a^{m-n}\)

Nếu người giữ vé số 47 trúng một trong bốn giải thì:
Người giữ vé số 47 có 4 cách chọn giải.
Ba giải còn lại ứng với một chỉnh hợp chấp 3 của 99 phần tử, do đó ta có A 99 3 = 941094 cách .
Vậy số kết quả bằng 4 × A 99 3 = 4 × 941094 = 3764376 kết quả.
Chọn đáp án D.