
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4.42:
a:=>x+y=0 và y-1=0
=>y=1 và x=-1
b: =>x-5=0 và 2y-7=0
=>x=5 và y=7/2

Bài 5:
1) Ta có: \(2x\left(x+1\right)-2x^2-2x\)
\(=2x^2+2x-2x^2-2x\)
=0
2) Ta có: \(3x\left(x-2\right)-3\left(x^2-2x\right)+4\)
\(=3x^2-6x-3x^2+6x+4\)
=4
3) Ta có: \(\left(x-1\right)\left(x-5\right)-x^2+6x-5\)
\(=x^2-6x+5-x^2+6x-5\)
=0
4) Ta có: \(\left(2x+1\right)\left(x-1\right)-2x^2+x-5\)
\(=2x^2-2x+x-1-2x^2+x-5\)
=-6
5) Ta có: \(\left(3x-2\right)\left(x-1\right)-3x^2+5x-4\)
\(=3x^2-3x-2x+2-3x^2+5x-4\)
=-2
6) Ta có: \(2x\left(x+1\right)-x\left(x+3\right)-x^2+x+5\)
\(=2x^2+2x-x^2-3x-x^2+x+5\)
=5

1)
\((x+2)(x+3)(x+4)(x+5)-24\\=[(x+2)(x+5)]\cdot[(x+3)(x+4)]-24\\=(x^2+7x+10)(x^2+7x+12)-24\)
Đặt \(x^2+7x+10=y\), khi đó biểu thức trở thành:
\(y(y+2)-24\\=y^2+2y-24\\=y^2+2y+1-25\\=(y+1)^2-5^2\\=(y+1-5)(y+1+5)\\=(y-4)(y+6)\\=(x^2+7x+10-4)(x^2+7x+10+6)\\=(x^2+7x+6)(x^2+7x+16)\)
2) Bạn xem lại đề!

A= 2006 X 2008 - 20072
A = 2006 . 2008 - 2007 . 2007
A = 2006 . ( 2007 + 1 ) - 2007 . ( 2006 + 1 )
A = 2006 . 2007 + 2006 - 2007 . 2006 + 2007
A = -1
B= 2016 X 2018 - 20172
B= 2016 . 2018 - 2017 . 2017
B = 2016 . ( 2017 + 1 ) - 2017 . ( 2016 + 1 )
B = 2016 . 2017 + 2016 - 2017 . 2016 + 2017
B = -1

\(\Leftrightarrow\left(x+3\right)^2\cdot\left(x-3\right)^2-6\left(x+3\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left[\left(x^2-9\right)\left(x-3\right)-6\right]=0\)
\(\Leftrightarrow\left(x+3\right)\left(x^3-3x^2-9x+21\right)=0\)
=>x+3=0
hay x=-3

Kẻ CH ⊥ BI và CH cắt BA tại D. Tam giác BCD có BH vừa là phân giác vừa là đường cao => Tam giác BCD cân tại B => BH là đường trung tuyến luôn => CH = DH. và DC = 2HC.
Đặt BC = x() Ta có: AD = BD - AB = BC - AB = x - 5
Gọi giao điểm của AC và BH là E.
Xét tam giác AEB và tam giác HEC có góc EAB = góc EHC = 90độ và góc AEB = góc HEC (đối đỉnh)
=> tam giác AEB ~ tam giác HEC(g.g)
=> Góc HCE = góc ABE.
=> Góc HCE = góc ABC/2 (1)
Mà Góc ECI = gócACB/2 (2)
Từ (1) và (2) => Góc ICH = Góc HCE + Góc ECI = (gócABC + góc ACB)/2 = 90độ/2 = 45độ.
Xét tam giác HIC có góc IHC = 90độ và Góc ICH = 45 độ (góc còn lại chắc chắn = 45 độ)
=> tam giác HIC vuông cân tại H => HI = HC.
Áp dụng đinh lý Py-ta-go cho tam giác này ta được: 2CH² = IC²
=> √2.CH = IC
=> CH = (IC)/(√2)
=> CH = 6/(√2)
=> DC = 2CH = 12/(√2) = 6√2
Xét tam giác: ADC có góc DAC = 90độ
=> Áp dụng định lý Py-ta-go ta có: DC² = AD² + AC²
=> AC² = DC² - AD²
=> AC² = (6√2)² - (x - 5)² (3)
Tương tự đối với tam giác ABC ta có: AC² = BC² - AB²
=> AC² = x² - 5² (4)
Từ (3) và (4) => (6√2)² - (x - 5)² = x² - 5²
<=> 72 - (x² - 10x + 25) = x² - 25
<=> 72 - x² + 10x - 25 - x² + 25 = 0
<=> -2x² + 10x + 72 = 0
<=> x² - 5x - 36 = 0
<=> x² - 9x + 4x - 36 = 0
<=> x(x - 9) + 4(x - 9) = 0
<=> (x - 9)(x + 4) = 0
<=> x - 9 = 0 hoặc x + 4 = 0
<=> x = 9 hoặc x = -4
=> chỉ có giá trị x = -9 là thoả mãn đk x > 5
=> BC = 5cm
b/ Tương tự ta tính được: CH = √5. => IH = √5 (cm)
=> BH = BI + IH = √5 + √5 = 2√5 (cm).
Xét tam giác BHC có góc BHC = 90độ => tính được BC = 5(cm). Kẻ IK ⊥ BC tại K.
Ta có IK = 1/2 đường cao hạ từ đỉnh H của tam giác BHC (chứng minh dựa vào tính chất đường trung bình).
=> IK.BC = S(BHC) = BH.HC/2
<=> IK.5 = 5
=> IK = 1(cm).
Xét tam giác BIK => tính được BK = 2 cm.
Kẻ IF vuông góc với AB => ta chứng minh đựơc BF = BK và AF = IF = IK
=> AB = (2 + 1)=3 (cm)
=> AC = 4cm

a: Xét ΔABC có
N là trung điểm của AC
M là trung điểm của BC
Do đó: NM là đường trung bình của ΔABC
Suy ra: NM//AB
hay ABMN là hình thang

`|x^2-5x|<6`
`<=>-6<x^2-5x<6`
`+)x^2-5x> -6`
`<=>x^2-5x+6>0`
`<=>(x-2)(x-3)>0`
`<=>x>3\or\x<2(1)`
`+)x^2-5x<6`
`<=>x^2-5x-6<0`
`<=>(x-6)(x+1)<0`
`<=>-1<x<6(2)`
`(1)(2)=>3<x<6\or\-1<x<2`

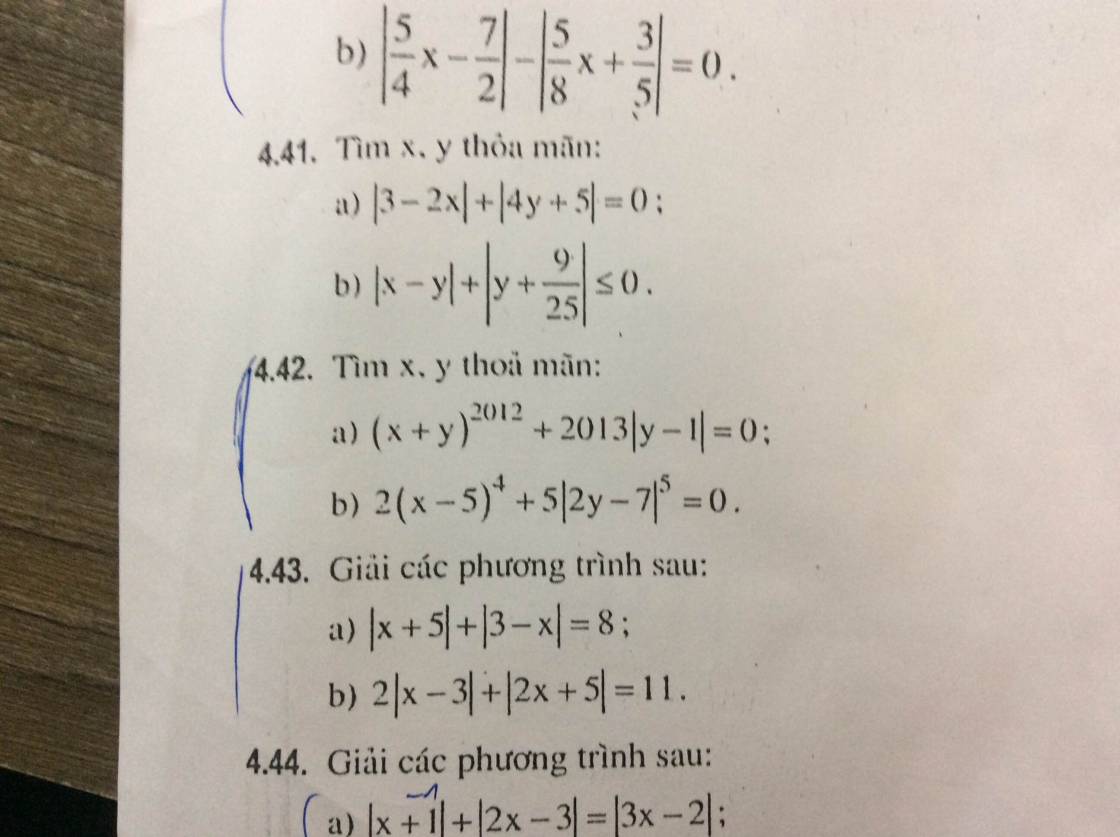


 Giúp mình nhé mọi người
Giúp mình nhé mọi người