TN
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HK
1
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 6 2021
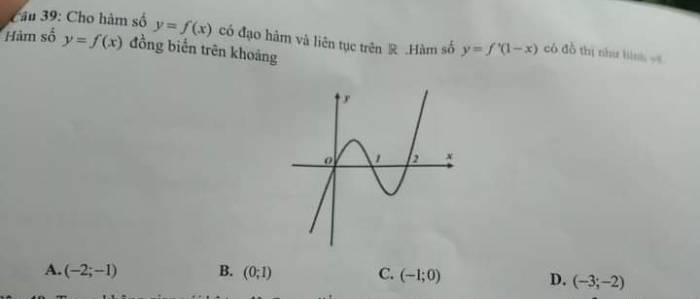
Đặt \(x=1-t\Rightarrow y=f\left(1-t\right)\Rightarrow y'=-f'\left(1-t\right)\) trái dấu với \(f'\left(1-t\right)\)
Từ đồ thị ta thấy \(f'\left(1-t\right)\) âm khi \(\left[{}\begin{matrix}t< 0\\1< t< 2\end{matrix}\right.\) hay \(y'\) dương khi \(\left[{}\begin{matrix}t< 0\\1< t< 2\end{matrix}\right.\)
Hay \(\left[{}\begin{matrix}1-x< 0\\1< 1-x< 2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x>1\\-1< x< 0\end{matrix}\right.\)
NM
Em có bài này muốn hỏi mọi người ạ, em đã cô lập được logy(x) nhưng tìm max min 2 ẩn vẫn khó quá :(.
2
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 5 2021
Đề bài liệu có chính xác không nhỉ? Mình chỉ có thể tìm được max bằng \(2\sqrt{2}\) (xảy ra khi \(lnx=\sqrt{2}\) và \(lny=\dfrac{1}{2}\)) và ko thể tìm được min.
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 5 2021
À rồi OK, suy nghĩ hơi cồng kềnh 1 xíu nên hướng tìm min bị sai:
Giả thiết tương đương: \(y^{\sqrt{4-ln^2x}}=x^{1-lny}\)
\(\Rightarrow\sqrt{4-ln^2x}.lny=\left(1-lny\right)lnx\) (1)
Do \(y\ne1\Rightarrow lny\ne0\)
Nên (1) tương đương: \(\sqrt{4-ln^2x}=\left(\dfrac{1-lny}{lny}\right)lnx\) (2)
Đặt \(\left\{{}\begin{matrix}lnx=a\\lny=b\end{matrix}\right.\) thì \(log_yx=\dfrac{a}{b}\)
(2) trở thành: \(\sqrt{4-a^2}=\left(\dfrac{1-b}{b}\right)a\)
\(\Rightarrow\sqrt{4-a^2}=\dfrac{a}{b}-a\Rightarrow\dfrac{a}{b}=\sqrt{4-a^2}+a\)
Xét hàm \(f\left(a\right)=\sqrt{4-a^2}+a\) trên \(\left[-2;2\right]\)
\(f'\left(a\right)=1-\dfrac{a}{\sqrt{4-a^2}}=0\Rightarrow a=\sqrt{2}\)
\(f\left(-2\right)=-2\) ; \(f\left(\sqrt{2}\right)=2\sqrt{2}\) ; \(f\left(2\right)=2\)
\(\Rightarrow f\left(a\right)_{min}=-2\) ; \(f\left(a\right)_{max}=2\sqrt{2}\)
Đáp án B
25 tháng 5 2019
Mấy bn đó đổi t.i.c.k hoặc trả lời nhiều
Mik vừa bị trừ 20đ hôm qua mà ko hiểu sao đây nè, đang cố kiếm lại
Chúc bn học tốt nha
_Shino_
T
25 tháng 5 2019
#)Trả lời :
Mọi ng làm thế này nek : https://www.youtube.com/watch?v=l6Anrb6r4dE
Cứ lên trên google gõ : cách hack điểm hỏi đáp trên olm là ra một đống, mk cho cái link video mak nhiều ng làm theo nhất đó !
Ae chớ nên học theo nha, không lợi lộc hay tốt đẹp j đâu ( mất cả hứng giải toán :v mk còn chưa dám hack mak sao nhiều ng hack giữ v ta ? )
#~Will~be~Pens~#
AH
Akai Haruma
Giáo viên
14 tháng 7 2020
Ai bảo bạn thế? Ví dụ hàm $f(x)=x^2+2x$ đồng biến trên $(-1;+\infty)$ nhưng nó có nghiệm $x=0$ lớn hơn $-1$ đấy.
Một nghìn không trăm hai mươi chín phẩy bốn trăm tám mươi sáu tỷ đồng
một nghìn không trăm hai mươi chín phẩy bốn trăm tám mươi sáu tỷ đồng