mng ơi thực sự mình rất cần bây giờ ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
E
1
8 tháng 8 2021
ta có sinB=\(\dfrac{AH}{AB}\)\(\Rightarrow\)AH=AB.sinB=3,6.sin62=3,18
BH=\(\sqrt{AB^2-AH^2}\)(pytago)=\(\sqrt{3,6^2-3,18^2}\)=1,69
\(_{\widehat{C}}\)=90-\(\widehat{B}\)=90-62=28\(^0\)
sinC=\(\dfrac{AB}{BC}\)\(\Rightarrow\)BC=\(\dfrac{AB}{sinC}\)=\(\dfrac{3,6}{sin28}\)=7,67
mà:CH=BC-BH=7,67-1,69=5,98
AC=\(\sqrt{BC^2-AB^2}\)(pytago)=\(\sqrt{7,67^2-3,6^2}\)=6.77
HK
1
PN
20 tháng 4 2022
DKXD : \(x\ge-1;y\ne-1\)
Dat : \(\left\{{}\begin{matrix}\sqrt{x+1}=a\left(a\ge0\right)\\y+1=b\left(b\ne0\right)\end{matrix}\right.\)
hpt<=>\(\left\{{}\begin{matrix}a+2-\dfrac{2}{y+1}=2\\2a-\dfrac{1}{y+1}=\dfrac{3}{2}\end{matrix}\right.\)
\(< =>\left\{{}\begin{matrix}a+2-\dfrac{2}{b}=2\\2a-\dfrac{1}{b}=\dfrac{3}{2}\end{matrix}\right.\)
\(< =>\left\{{}\begin{matrix}a-\dfrac{2}{b}=0\\4a-\dfrac{2}{b}=3\end{matrix}\right.< =>\left\{{}\begin{matrix}3a=3\\a=\dfrac{2}{b}\end{matrix}\right.< =>\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\)(tmdk)
\(=>\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)(tmdk)
LB
1
22 tháng 9 2021
2:
a: Xét tứ giác DIHK có
\(\widehat{DIH}=\widehat{DKH}=\widehat{IDK}=90^0\)
Do đó: DIHK là hình chữ nhật
Suy ra: DH=KI(1)
Xét ΔDEF vuông tại D có DH là đường cao ứng với cạnh huyền EF
nên \(DH^2=HE\cdot HF\left(2\right)\)
Từ (1) và (2) suy ra \(IK^2=HE\cdot HF\)
9 tháng 4 2022
\(=\dfrac{\sqrt{a}+2+\sqrt{a}-2}{a-4}:\dfrac{\sqrt{a}+2-2}{\sqrt{a}+2}\)
\(=\dfrac{2\sqrt{a}}{a-4}\cdot\dfrac{\sqrt{a}+2}{\sqrt{a}}=\dfrac{2}{\sqrt{a}-2}\)
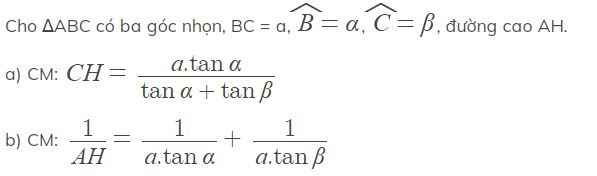
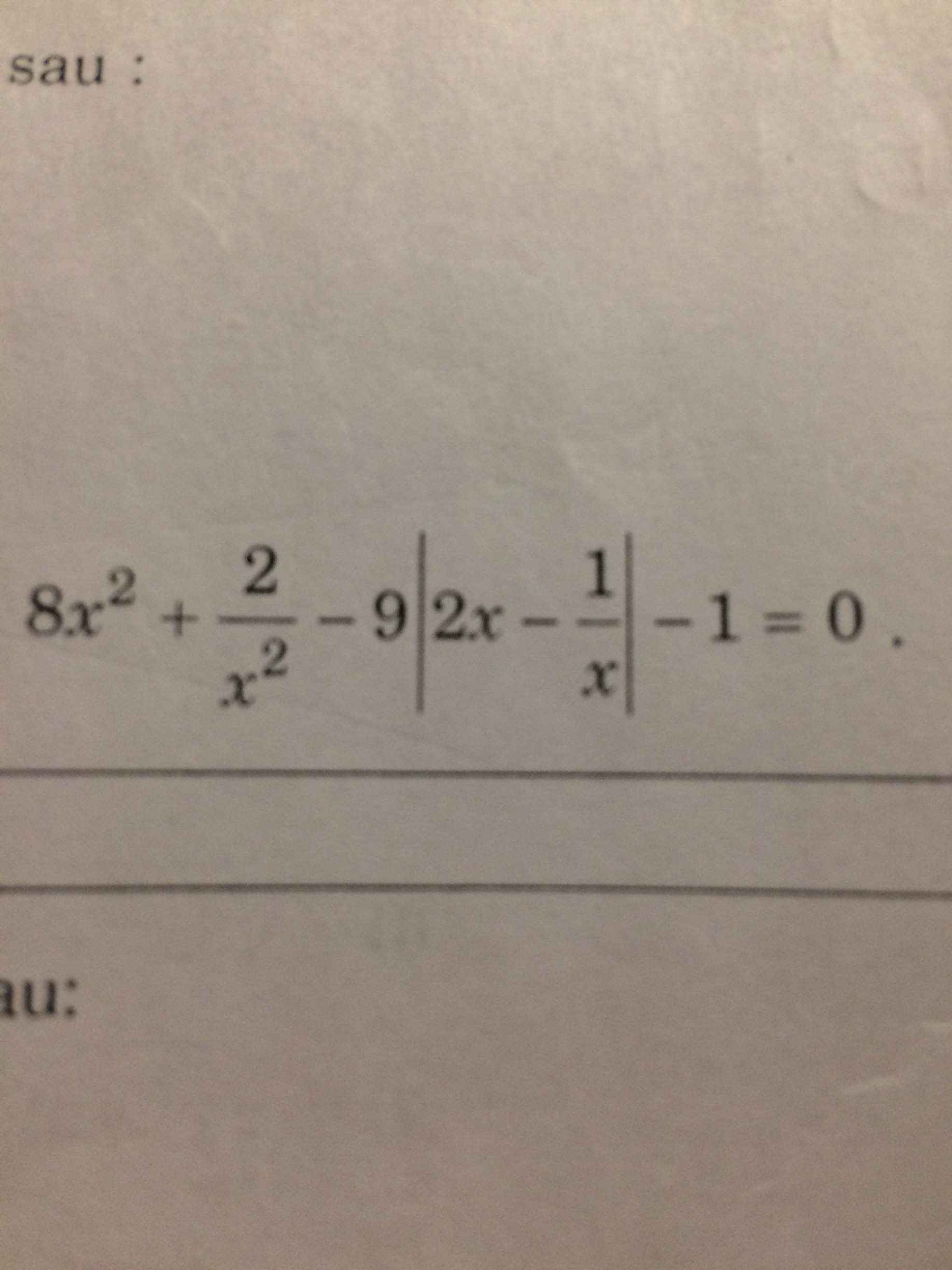
Giúp mình giải với mng ơi chiều mình cần gấppp
Nửa chu vi hình chữ nhật : 42 : 2 = 21(m)
Gọi x(m) là chiều dài hình chữ nhật ( 10 < x < 21 )
=> Chiều rộng hình chữ nhật = 21 - x (m)
Theo đlí Pythagoras ta có : x2 + ( 21 - x )2 = 152
<=> x2 + x2 - 42x + 441 - 225 = 0
<=> 2x2 - 42x + 216 = 0
<=> x2 - 21x + 108 = 0 <=> ( x - 12 )( x - 9 ) = 0
<=> x = 12 (tm) hoặc x = 9 (ktm)
=> Chiều dài = 12m ; chiều rộng 9m