Cho nửa đường tròn tâm O đường kính AB, kẻ tiếp tuyến Ax (Ax và nửa đường tròn nằm trên cùng nửa mặt phẳng bờ AB). Trên tia đối của tia BA lấy C, kẻ tiếp tuyến CE với (O), tia CE cắt tia Ax tại D(E là tiếp điểm). DO cắt AE tại H1) Chứng minh OD//BE2) Gọi K là giao điểm của DB với (O). Chứng minh DE²=DK.DB và tứ giác KHOB nội tiếp đường tròn3) Đường thẳng vuông góc với AB tại O cắt CD...
Đọc tiếp
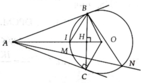
Cho nửa đường tròn tâm O đường kính AB, kẻ tiếp tuyến Ax (Ax và nửa đường tròn nằm trên cùng nửa mặt phẳng bờ AB). Trên tia đối của tia BA lấy C, kẻ tiếp tuyến CE với (O), tia CE cắt tia Ax tại D(E là tiếp điểm). DO cắt AE tại H
1) Chứng minh OD//BE
2) Gọi K là giao điểm của DB với (O). Chứng minh DE²=DK.DB và tứ giác KHOB nội tiếp đường tròn
3) Đường thẳng vuông góc với AB tại O cắt CD và đường thẳng BE tại M và N; I là giao điểm của AN và OD, J là giao điểm của DN và OE. Chứng minh M, I, J thẳng hàng

a) \(OB=OC\)nên \(O\)thuộc đường trung trực của \(BC\)
\(AB=AC\)nên \(A\)thuộc đường trung trực của \(BC\)
suy ra \(AO\)là đường trung trực của \(BC\).
b) Xét tam giác \(ABO\)vuông tại \(B\)đường cao \(BH\):
\(AB^2=AH.AO\)
Xét tam giác \(ABM\)và tam giác \(ANB\):
\(\widehat{A}\)chung
\(\widehat{ABM}=\widehat{ANB}\)
suy ra \(\Delta ABM~\Delta ANB\left(g.g\right)\)
\(\Rightarrow\frac{AB}{AN}=\frac{AM}{AB}\Rightarrow AB^2=AM.AN\)
Suy ra \(AH.AO=AM.AN\).