
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các câu hỏi dưới đây có thể giống với câu hỏi trên
SG
3

LD
12 tháng 3 2018
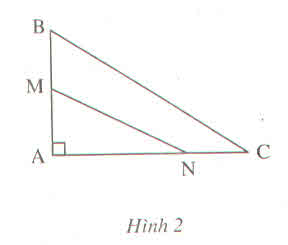
Hình chiếu của AN < hình chiếu của AC
=> đường xiên BN < đường xiên của BC (1)
Hình chiếu của AM < hình chiếu AB => đường xiên MN < đường xiên NB. (2)
Từ (1) và (2) suy ra:
MN< BN< BC.
SG
1

DN
12 tháng 5 2017
| Giá trị (x) | Tần số (n) | Các tích (x.n) | |
| 17 | 3 | 51 | |
| 18 | 5 | 90 | |
| 19 | 4 | 76 | |
| 20 | 2 | 40 | |
| 21 | 3 | 63 | |
| 22 | 2 | 44 | |
| 24 | 3 | 72 | |
| 26 | 3 | 78 | |
| 28 | 1 | 28 | |
| 30 | 1 | 30 | |
| 31 | 2 | 62 | |
| 32 | 1 | 32 | |
| N = 30 | Tổng: 666 |

25 tháng 10 2017
| Phép tính | Ước lương kết quả | ĐS đúng |
| 24.68:12 | 20.70:10 = 140 | 136 |
| 7,8.3,1:1,6 | 8.3:2=12 | 15,1125 |
| 6,9.72:24 | 7.70:20 = 24,5 | 20,7 |
| 56.9,9:8,8 | 60.10:9 = 66,(6) | 63 |
| 0,38.0,45:0,95 | 0.0:1=0 | 0,18 |












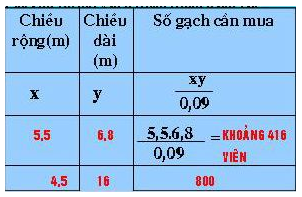

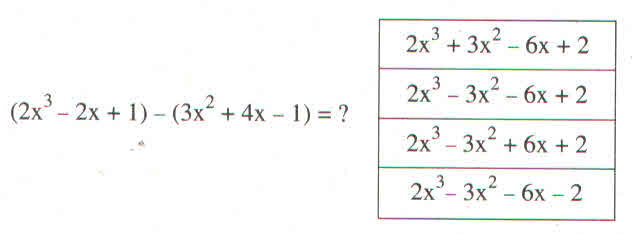


cái đề khó nhìn quá. Bạn gửi hình khác rõ hơn được ko.