Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)\({-1\over 2}x^2×y^2 - x^2×y^2 +{2\over 3} x^2×y^2 \)
=\(({ -1\over 2}-1+{ 2\over 3})x^2×y^2\)
=\({-5 \over 6}x^2×y^2\)
b)\({1 \over 2}a^3×b^2 +{4 \over 3}3ab^2 × {1 \over 2}a^2\)
=\({1 \over 2}a^3×b^2 +({4 \over 3}× {1 \over 2})3b^2 (a×a^2) \)
=\({1 \over 2}a^3×b^2 +{2 \over 3}3a^3b^2\)
=\(({1 \over 2} +{2 \over 3}3)a^3b^2\)
=\({5 \over 2}a^3b^2\)
c)

Áp dụng t/c dãy tỉ số bằng nhau:
a.
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{2x}{6}=\dfrac{4y}{20}=\dfrac{2x+4y}{6+20}=\dfrac{28}{26}=\dfrac{14}{13}\)
\(\Rightarrow\left\{{}\begin{matrix}x=3.\dfrac{14}{13}=\dfrac{52}{13}\\y=5.\dfrac{14}{13}=\dfrac{70}{13}\end{matrix}\right.\)
(Em có nhầm đề 26 thành 28 ko nhỉ, số xấu quá)
b.
\(4x=5y\Rightarrow\dfrac{x}{5}=\dfrac{y}{4}=\dfrac{3x}{15}=\dfrac{-2y}{-8}=\dfrac{3x-2y}{15-8}=\dfrac{35}{7}=5\)
\(\Rightarrow\left\{{}\begin{matrix}x=5.5=25\\y=4.2=20\end{matrix}\right.\)
c.
\(\dfrac{x}{-3}=\dfrac{y}{-7}=\dfrac{2x}{-6}=\dfrac{4y}{-28}=\dfrac{2x+4y}{-6-28}=\dfrac{68}{-34}=-2\)
\(\Rightarrow\left\{{}\begin{matrix}x=-3.\left(-2\right)=6\\y=-7.\left(-2\right)=14\end{matrix}\right.\)
d.
\(\dfrac{x}{2}=\dfrac{y}{-3}=\dfrac{z}{4}=\dfrac{4x}{8}=\dfrac{-3y}{9}=\dfrac{-2z}{-8}=\dfrac{4x-3y-2z}{8+9-8}=\dfrac{16}{9}\)
\(\Rightarrow\left\{{}\begin{matrix}x=2.\dfrac{16}{9}=\dfrac{32}{9}\\y=-3.\dfrac{16}{9}=-\dfrac{48}{9}\\z=4.\dfrac{16}{9}=\dfrac{64}{9}\end{matrix}\right.\)

\(\frac{x}{3}=\frac{y}{4}\Rightarrow\frac{x^2}{9}=\frac{y^2}{16}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có :
\(\frac{x^2}{9}=\frac{y^2}{16}=\frac{x^2+y^2}{9+16}=\frac{100}{25}=4\)
Suy ra :
+) \(\frac{x}{3}=4\Rightarrow x=12\)
+) \(\frac{y}{4}=4\Rightarrow y=16\)


Lần sau bạn nhớ đánh đề rõ ràng hơn. Nếu nhìn đề thì mình nghĩ thế này
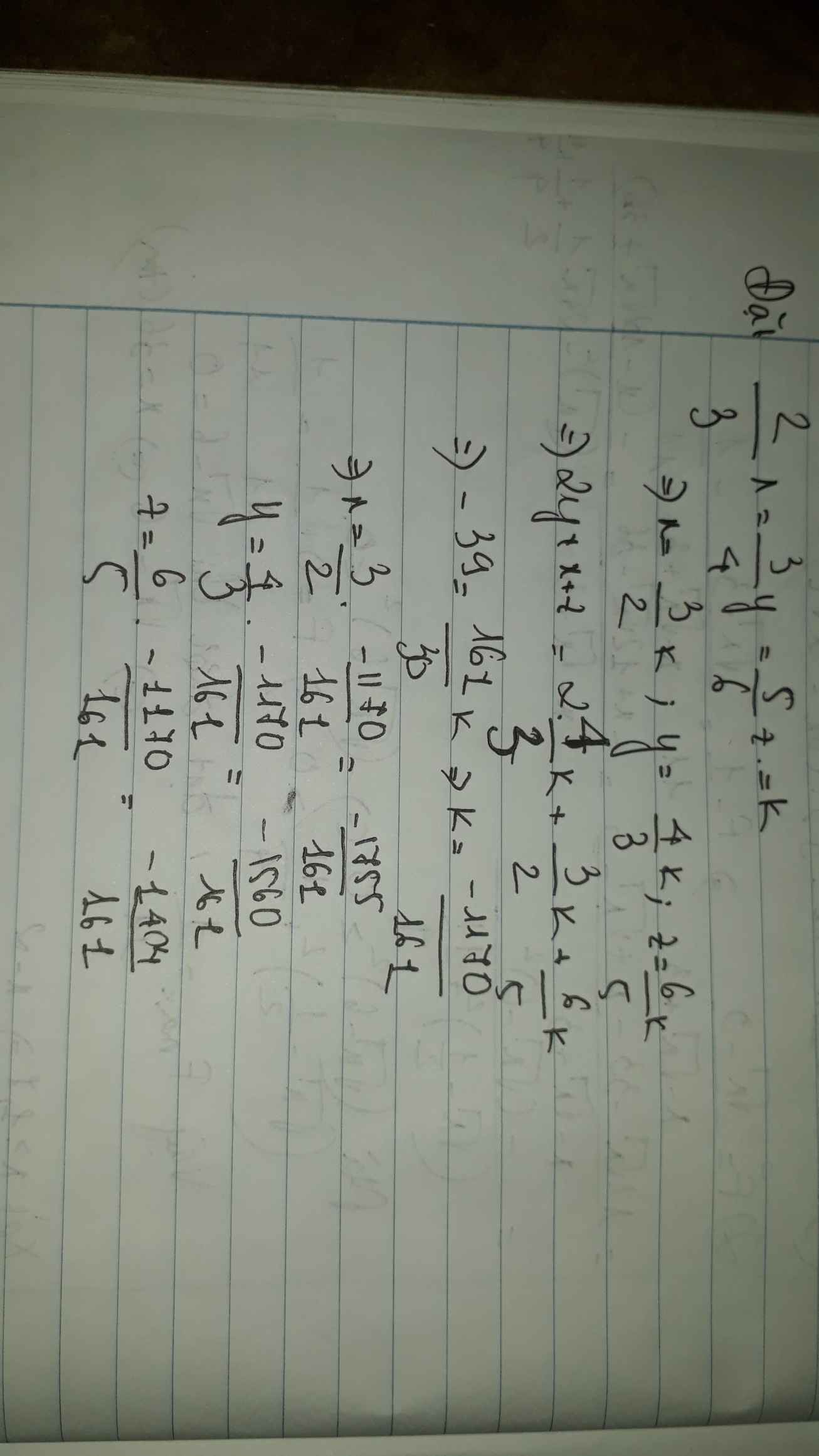

Câu 2:
\(A\left(x\right)=x^2+3x+1\)
\(B\left(x\right)=2x^2-2x-3\)
a) Tính A(x) là sao em?
b) \(A\left(x\right)+B\left(x\right)=\left(x^2+3x+1\right)+\left(2x^2-2x-3\right)\)
\(=x^2+3x+1+2x^2-2x-3\)
\(=\left(x^2+2x^2\right)+\left(3x-2x\right)+\left(1-3\right)\)
\(=3x^2+x-2\)
Câu 1:
\(M\left(x\right)=x^3+3x-2x-x^3+2\)
\(=\left(x^3-x^3\right)+\left(3x-2x\right)+2\)
\(=x+2\)
Bậc của M(x) là 1
chắc b