K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 1 2022
a: Xét tứ giác BFCE có
D là trung điểm của BC
D là trung điểm của FE
Do dó: BFCE là hình bình hành
b: Xét tứ giác ABFE có
AB//FE
AB=FE
Do đó: ABFE là hình bình hành
mà \(\widehat{FAB}=90^0\)
nên ABFE là hình chữ nhật
30 tháng 7 2023
a: AN+CN=AC
=>AN=20-15=5cm
Xét ΔABC có AM/AB=AN/AC
nên MN//BC
b: Xét ΔAMN và ΔNPC có
góc AMN=góc NPC(=góc B)
góc ANM=góc NCP)
=>ΔAMN đồng dạng với ΔNPC
26 tháng 7 2023
1: AD=8-2=6cm
AD/AB=6/8=3/4
AE/AC=9/12=3/4
=>AD/AB=AE/AC
2: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc A chung
=>ΔADE đồng dạng với ΔABC
3: AI là phân giác
=>IB/IC=AB/AC
=>IB/IC=AD/AE
=>IB*AE=AD*IC
NV
0
DT
3
2 tháng 8 2021
8) \(\dfrac{x+7}{3}+\dfrac{x+5}{4}=\dfrac{x+3}{5}+\dfrac{x+1}{6}\)
\(\Rightarrow\dfrac{x+7}{3}+\dfrac{x+5}{4}-\dfrac{x+3}{5}-\dfrac{x+1}{6}=0\)
\(\Rightarrow\dfrac{x+7}{3}+2+\dfrac{x+5}{4}+2-\dfrac{x+3}{5}-2-\dfrac{x+1}{6}-2=0+2+2-2-2\)
\(\Rightarrow\left(\dfrac{x+7}{3}+2\right)+\left(\dfrac{x+5}{4}+2\right)-\left(\dfrac{x+3}{5}+2\right)-\left(\dfrac{x+1}{6}+2\right)=0\)
\(\Rightarrow\left(\dfrac{x+7}{3}+\dfrac{6}{3}\right)+\left(\dfrac{x+5}{4}+\dfrac{8}{4}\right)-\left(\dfrac{x+3}{5}+\dfrac{10}{5}\right)-\left(\dfrac{x+1}{6}+\dfrac{12}{2}\right)=0\)
\(\Rightarrow\left(x+13\right)\left(\dfrac{1}{3}+\dfrac{1}{4}-\dfrac{1}{5}-\dfrac{1}{6}\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+13=0\\\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}=0\end{matrix}\right.\)
\(x+13=0\)
\(\Rightarrow x=-13\)
\(\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}=0\)
\(\dfrac{13}{60}=0\) (vô lí)
Vậy \(x=-13\)
9) Bạn chuyển vế rồi cộng 3 vào từng mỗi số
D
19 tháng 1 2022
- Đây có phải là toán lớp 8 nữa không vậy :)? Mình học toán nâng cao nhưng chưa bao giờ thấy dạng này :).
DT
19 tháng 1 2022
b1:
do x;y thuộc số nguyên N và x,y\(\ge\)2
=>\(-4xy+1< +7x-7y< 4xy+1\)
\(\Rightarrow4x^2y^2-4xy+1< 4x^2y^2+7x-7y< 4x^2y^2+4xy+1\)
\(\Rightarrow\left(2xy-1\right)^2< 4x^2y^2+7x-7y< \left(2xy+1\right)^2\)
mà \(4x^2y^2+7x-7y\) là số chính phương và 1<2xy-1<2xy-1 nên ta có:
\(4x^2y^2+7x-7y-\left(2xy\right)^2\Leftrightarrow x=y\)
14 tháng 7 2023
5:
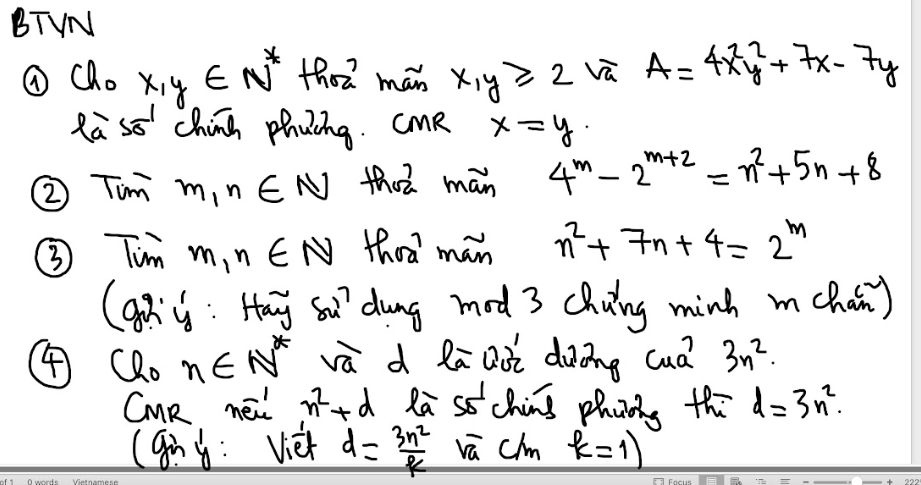
\(\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}>=3\cdot\sqrt[3]{\dfrac{a}{b}\cdot\dfrac{b}{c}\cdot\dfrac{c}{a}}=3\)
a^2+b^2>=2ab
b^2+c^2>=2bc
a^2+c^2>=2ac
=>a^2+b^2+c^2>=ab+bc+ac
=>(ab+bc+ac)/(a^2+b^2+c^2)>=1
=>a/b+b/c+c/a+(ab+ac+bc)/(a^2+b^2+c^2)>=4
Bài 4 :
\(B=\left(9+1\right)\left(9^2+1\right)...\left(9^{32}+1\right)\)
\(8B=\left(9^2-1\right)\left(9^2+1\right)...\left(9^{32}+1\right)=9^{64}-1\)
\(\Rightarrow B=\frac{9^{64}-1}{8}< 9^{64}-1\Rightarrow B< C\)
bài 5mn giúp em đc k ạ