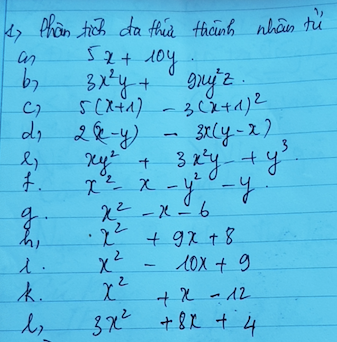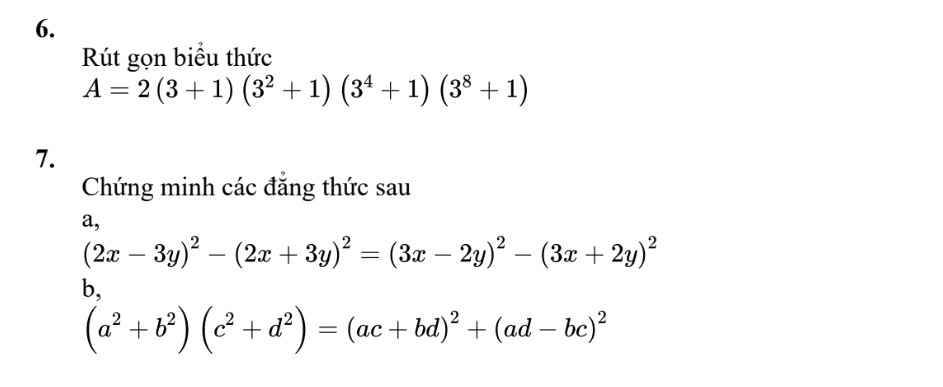Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a, Ta có: AM = MD (gt), BN=CN (gt)
=> MN là đường trung bình của hình thang ABCD
=>\(MN=\frac{AB+CD}{2}\Rightarrow AB+8=6.2\Rightarrow AB=12-8=4\left(cm\right)\)
b, MN là đường trung bình của hình thang ABCD
=> MN // AB
Mà AM = MD (gt)
=> MP là đường trung bình của t/g ABD
=> \(MP=\frac{AB}{2}=\frac{4}{2}=2\left(cm\right)\)
Lại có: MN // AB, BN=CN(gt)
=>NQ là đường trung bình cuat t/g ABC
=>\(NQ=\frac{AB}{2}=\frac{4}{2}=2\left(cm\right)\)
=> PQ = MN - MQ - NQ = 6 - 2 - 2 = 2 (cm)
Vậy...

a,\(5x+10y=5\left(x+2y\right)\)
b,\(=3xy\left(x+3yz\right)\)
c,\(=\left(x+1\right)\left(5-3x-3\right)=\left(x+1\right)\left(2-3x\right)\)
d,\(=\left(x-y\right)\left(2+3x\right)\)
e,\(=y\left(xy+3x^2+y^2\right)\)
f,\(=\left(x-y\right)\left(x+y\right)-\left(x+y\right)=\left(x+y\right)\left(x-y-1\right)\)
g,\(=x^2-x+\dfrac{1}{4}-\left(\dfrac{5}{2}\right)^2=\left(x-\dfrac{1}{2}\right)^2-\left(\dfrac{5}{2}\right)^2=\left(x-3\right)\left(x+2\right)\)
h,\(=x^2+9x+\dfrac{81}{4}-\left(\dfrac{7}{2}\right)^2=\left(x+\dfrac{9}{2}\right)^2-\left(\dfrac{7}{2}\right)^2=\left(x+1\right)\left(x+8\right)\)
i,\(=x^2-10x+25-4^2=\left(x-5\right)^2-4^2=\left(x-1\right)\left(x-9\right)\)
k,\(=x^2+x+\dfrac{1}{4}-\left(\dfrac{7}{2}\right)^2=\left(x+\dfrac{1}{2}\right)^2-\left(\dfrac{7}{2}\right)^2=\left(x-3\right)\left(x+4\right)\)
l.\(=3\left(x^2+\dfrac{8}{3}x+\dfrac{4}{3}\right)=3\left(x^2+\dfrac{8}{3}x+\dfrac{16}{9}-\dfrac{4}{9}\right)\)
\(=3[\left(x+\dfrac{4}{3}\right)^2-\left(\dfrac{2}{3}\right)^2]=3\left(x+\dfrac{2}{3}\right)\left(x+2\right)\)

\(7,\) \(a,\left(2x-3y\right)^2-\left(2x+3y\right)^2=\left(3x-2y\right)^2-\left(3x+2y\right)^2\)
\(\Leftrightarrow4x^2-12xy+9y^2-4x^2-12xy-9y^2=9x^2-12xy+4y^2-9x^2-12xy-4y^2\)
\(\Leftrightarrow-24xy=-24xy\) ( luôn đúng )
Vậy 2 đẳng thức ở 2 vế bằng nhau.
\(b,\left(a^2+b^2\right)\left(c^2+d^2\right)=\left(ac+bd\right)^2+\left(ad-bc\right)^2\)
\(\Leftrightarrow\left(ac\right)^2+\left(ad\right)^2+\left(bc\right)^2+\left(bd\right)^2=\left(ac\right)^2+2acbd+\left(bd\right)^2+\left(ad\right)^2-2adbc+\left(bc\right)^2\)
\(\Leftrightarrow\left(ac\right)^2+\left(ad\right)^2+\left(bc\right)^2+\left(bd\right)^2=\left(ac\right)^2+\left(ad\right)^2+\left(bc\right)^2+\left(bd\right)^2\) ( luôn đúng )
Vậy 2 đẳng thức ở 2 vế bằng nhau.
*Ở câu \(b,\) dòng thứ 3, vế phải triệt tiêu \(2acbd-2adbc\) \(=0\) nên mất rồi nha.

Bài 5:
Áp dụng BĐT Cô-si cho các số không âm:
$a^4+b^4\geq 2a^2b^2$
$c^4+d^4\geq 2c^2d^2$
$2(a^2b^2+c^2d^2)\geq 4\sqrt{a^2b^2c^2d^2}=4|abcd|\geq 4abcd$
$\Rightarrow a^4+b^4+c^4+d^4\geq 4abcd$
Ta có đpcm
Dấu "=" xảy ra khi $|a|=|b|=|c|=|d|$ và $ab=cd$
Bài 1:
Đổi $30$ phút thành $0,5$ giờ
Thời gian đi từ $A$ đến $B$ là:
$t_1=\frac{AB}{40}$ (h)
Thời gian đi từ $B$ về $A$ là:
$t_2=\frac{BA}{45}$ (h)
Theo bài ra ta có:
$t_1-t_2=\frac{AB}{40}-\frac{AB}{45}$
$0,5=\frac{AB}{360}$
$\Rightarrow AB=180$ (km)

k phải gắn nhaaa
gãy là ngta bó bột lại cho đến khi khỏi
giúp ngta nà