K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
5 tháng 8 2023
a: A=x^2+4x+4+5
=(x+2)^2+5>=5
Dấu = xảy ra khi x=-2
b: =3/2(x^2+2/3x+2/3)
=3/2(x^2+2*x*1/3+1/9+5/9)
=3/2(x+1/3)^2+15/18>=15/18=5/6
Dấu = xảy ra khi x=-1/3
e: =x^2-2x+1+4
=(x-1)^2+4>=4
Dấu = xảy ra khi x=1
f: =2(x^2-3x)
=2(x^2-3x+9/4-9/4)
=2(x-3/2)^2-9/2>=-9/2
Dấu = xảy ra khi x=3/2
h: =-(x^2-4x-3)
=-(x^2-4x+4-7)
=-(x-2)^2+7<=7
Dấu = xảy ra khi x=2
NT
1
30 tháng 7 2023
a: AN+CN=AC
=>AN=20-15=5cm
Xét ΔABC có AM/AB=AN/AC
nên MN//BC
b: Xét ΔAMN và ΔNPC có
góc AMN=góc NPC(=góc B)
góc ANM=góc NCP)
=>ΔAMN đồng dạng với ΔNPC
NT
0
1 tháng 10 2017
\(2x^2+2y^2-4xy+2x-2y+4\)
\(=2\left(x-y\right)^2+2\left(x-y\right)+4\)
\(=2\left[\left(x-y\right)^2+2\left(x-y\right)\frac{1}{2}+\frac{1}{4}\right]+\frac{7}{2}\)
\(=2\left(x-y+\frac{1}{2}\right)^2+\frac{7}{2}\)
\(\Rightarrow A\ge\frac{7}{2}\)
Dấu = bn tự tính nhé
NH
3
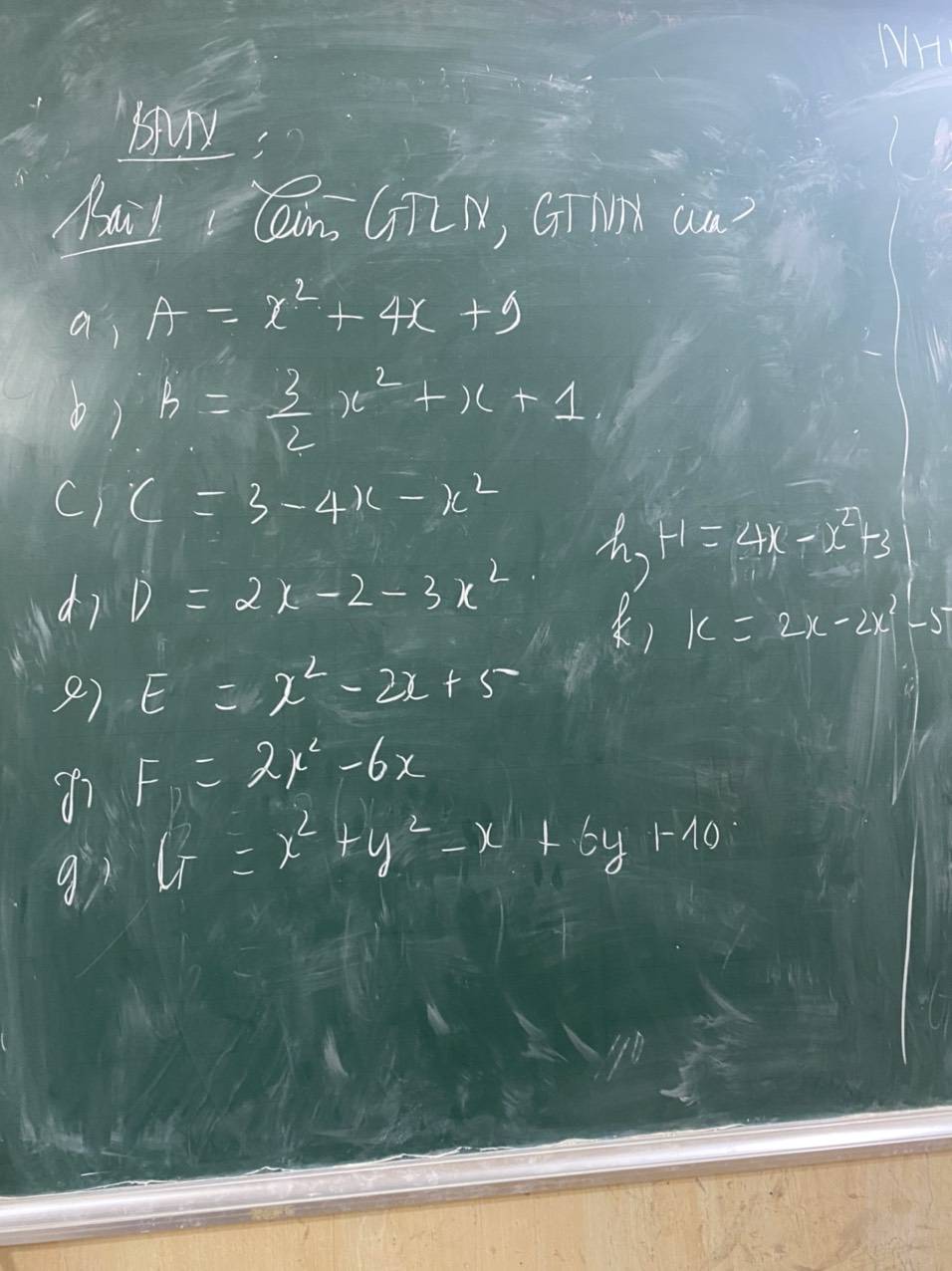
a, Áp dụng định lý Ta-lét ta có:
\(\dfrac{AD}{DB}=\dfrac{AE}{EC}\Rightarrow\dfrac{4}{x}=\dfrac{5}{10}\Rightarrow x=4:\dfrac{1}{2}\Rightarrow x=8\)
Áp dụng hệ quả định lý Ta-lét ta có:
\(\dfrac{AE}{AC}=\dfrac{DE}{BC}\Rightarrow\dfrac{5}{15}=\dfrac{6}{y}\Rightarrow y=6:\dfrac{1}{3}\Rightarrow y=18\)
b, Áp dụng định lý phân giác ta có:
\(\dfrac{DB}{DC}=\dfrac{AB}{AC}\Rightarrow\dfrac{5}{6}=\dfrac{10}{x}\Rightarrow x=10:\dfrac{5}{6}\Rightarrow x=12\)