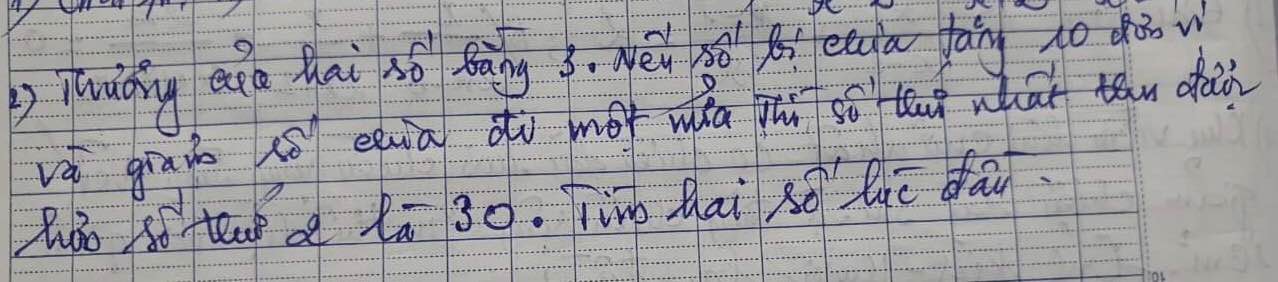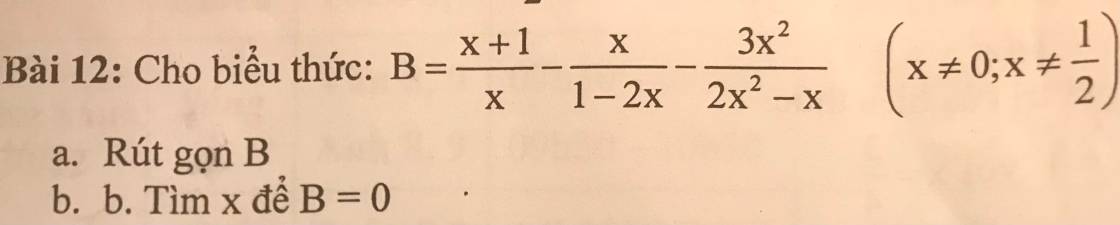Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2:
a: BC=căn 6^2+8^2=10cm
Xét ΔBAC có BD là phân giác
nên AD/AB=DC/BC
=>AD/3=DC/5=(AD+DC)/(3+5)=8/8=1
=>AD=3cm; DC=5cm
b: Xét ΔBAD vuông tại A và ΔBHI vuông tại H có
góc ABD=góc HBI
=>ΔBAD đồng dạng với ΔBHI
=>BA/BH=BD/BI
=>BA*BI=BH*BD
c: góc ADI=góc HIB
góc AID=góc HIB
=>góc AID=góc ADI
=>ΔADI cân tại A

a) \(\Leftrightarrow\left(-63x^2+78x-15\right)+\left(63x^3+x-20\right)=44\)
\(\Leftrightarrow-63x^2+78x-15+63x^2+x-20=44\)
\(\Leftrightarrow79x-35=44\)
\(\Leftrightarrow79x=44+35\)
\(\Leftrightarrow79x=79\)
\(\Leftrightarrow x=1\)
b) \(\Leftrightarrow\left(x^2+3x+2\right).\left(x+5\right)-x^2.\left(x+8\right)=27\)
\(\Leftrightarrow x.\left(x^2+3x+2\right)+5.\left(x^2+3x+2\right)-x^3-8x^2=27\)
\(\Leftrightarrow x^3+3x^2+2x+5x^2+15x+10-x^3-8x^2=27\)
\(\Leftrightarrow17x+10=27\)
\(\Leftrightarrow17x=17\)
\(\Leftrightarrow x=1\)

Gọi tử là x
Mẫu là x+11
Theo đề, ta có:
\(\dfrac{x+3}{x+7}=\dfrac{3}{4}\)
=>4x+12=3x+21
hay x=9
Vậy: Phân số ban đầu là 9/20





a: \(=\dfrac{\left(x+1\right)\left(2x-1\right)+x^2-3x^2}{x\left(2x-1\right)}\)
\(=\dfrac{2x^2-x+2x-1+\left(-2x^2\right)}{x\left(2x-1\right)}\)
\(=\dfrac{x-1}{x\left(2x-1\right)}\)
b: Để B=0 thì x-1=0
=>x=1

Bạn chỉ cần áp dụng cái phân tích đa thức thành nhân tử bằng phương pháo đặt nhân tử chung là ra rồi

b: Xét ΔABD và ΔBAC có
BA chung
BD=AC
AD=BC
Do đó: ΔABD=ΔBAC
c: ta có: EA+EC=AC
EB+ED=BD
mà AC=BD
và EA=EB
nên EC=ED