DV
6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LT
1
TN
15 tháng 7 2016
tr 10h à còn sớm
P=x2 - 2x + 5
=x2-2x+1+4
=(x-1)2+4
Ta thấy:\(\left(x-1\right)^2+4\ge0+4=4\)
Dấu = khi x=1
Vậy Pmin=4 <=>x=1
Q= 2x2 -6x
\(=2x^2-6x+\frac{9}{2}-\frac{9}{2}\)
\(=2\left(x^2-3x+\frac{9}{4}\right)-\frac{9}{2}\)
\(=2\left(x-\frac{3}{2}\right)\left(x-\frac{3}{2}\right)-\frac{9}{2}\)
\(=2\left(x-\frac{3}{2}\right)^2-\frac{9}{2}\)
Ta thấy:\(2\left(x-\frac{3}{2}\right)^2-\frac{9}{2}\ge0-\frac{9}{2}=-\frac{9}{2}\)
Dấu = khi x=3/2
Vậy Qmin=-9/2 <=>x=3/2
15 tháng 7 2016
P = x2 - 2x + 5 = x(x - 2) + 5 nhỏ nhất khi x(x - 2) nhỏ nhất .
Xét x(x - 2) < 0 (để nhỏ nhất) thì x và x - 2 khác dấu mà x > x - 2 nên x > 0 > x - 2 => 2 > x > 0 => x = 1 => x(x - 2) = -1
Vậy P min = -1 + 5 = 4
Q = 2x2 - 6x = 2x(x - 3) nhỏ nhất khi x(x - 3) nhỏ nhất
Xét x(x - 3) < 0 (để nhỏ nhất) thì x và x - 3 khác dấu mà x > x - 3 nên x > 0 > x - 3 => 3 > x > 0 => x = 1;2
Ta thấy x(x - 3) = -2 tại x = 1 và x = 2 nên [x(x - 3)]min = -2 => Qmin = -2.2 = -4
16 tháng 4 2023
=>3(x-1)-2(x-2)<=6/4(x-3)
=>3x-3-2x+4<=3/2x-9/2
=>-1/2x<=-9/2-1=-11/2
=>x>=11
14 tháng 8 2021
d: \(\left(\dfrac{1}{2}x-1\right)\left(2x-3\right)\)
\(=x^2-\dfrac{3}{2}x-2x+3\)
\(=x^2-\dfrac{7}{2}x+3\)
e: Ta có: \(\left(x-7\right)\left(x-5\right)\)
\(=x^2-5x-7x+35\)
\(=x^2-12x+35\)
f: Ta có: \(\left(x-\dfrac{1}{2}\right)\left(x+\dfrac{1}{2}\right)\left(4x-1\right)\)
\(=4\left(x-\dfrac{1}{4}\right)\left(x-\dfrac{1}{4}\right)\)
\(=4\left(x-\dfrac{1}{4}\right)^2\)
\(=4\left(x^2-\dfrac{1}{2}x+\dfrac{1}{16}\right)\)
\(=4x^2-2x+\dfrac{1}{4}\)
LT
2
26 tháng 2 2022
a: \(BC=\sqrt{AB^2+AC^2}=20\left(cm\right)\)
Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/12=CD/16
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{12}=\dfrac{CD}{16}=\dfrac{BD+CD}{12+16}=\dfrac{20}{28}=\dfrac{5}{7}\)
Do đó: BD=60/7(cm); CD=80/7(cm)
b: \(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{12\cdot16}{20}=9.6\left(cm\right)\)
26 tháng 2 2022
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
B C 2 = A B 2 + A C 2 = 12 2 + 6 2 = 400
Suy ra: BC =20 (cm)
Vì AD là đường phân giác của ∠(BAC) nên:
\(\dfrac{DB}{DC}=\dfrac{AB}{AC}\) (tính chất đường phân giác)
Suy ra: 
Suy ra: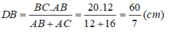 
Vậy : DC = BC – DB = 20 - 60/7 = 80/7 (cm)
25 tháng 8 2021
\(\left|-5x\right|-16=3x\Leftrightarrow\left|-5x\right|=3x+16\)ĐK : x > = -16/3
TH1 : \(-5x=3x+16\Leftrightarrow-8x=16\Leftrightarrow x=-2\)
TH2 : \(-5x=-3x-16\Leftrightarrow-2x=-16\Leftrightarrow x=8\)
NV
1
26 tháng 9 2017
Đặt A=3(22+1)(24+1)...(264+1) +1
<=> A= (2+1)(22+1)(24+1)...(264+1) +1
<=>(2-1)A=(2-1)(2+1)(22+1)(24+1)...(264+1) +1
<=>1A=(22-1)(22+1)(24+1)...(264+1) +1
<=>A =(24 -1)(24+1)...(264+1) +1
........
<=> A=(264-1)(264+1) +1
<=> A= 2128-1+1 = 2128
Vậy A= 2128
NV
0
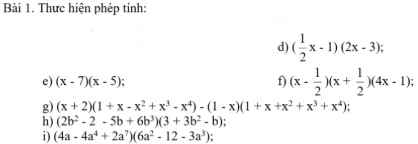
\(x^2+2xy-8y^2+2xz+14yz-3z^2\)
\(=\left(x^2+y^2+z^2+2xy+2yz\right)+\left(-9x^2-12yz-4x^2\right)\)
\(=\left(x+y+z\right)^2-[\left(3x\right)2-2.3x2y+\left(2x\right)^2\)
\(=\left(x+y+z\right)^2-\left(3y-2x\right)^2\)
\(=\left(x+y+z-3y+2x\right)\left(x+y+z+3y-2x\right)\)
\(3x^2-22xy-4x+8y+7y^2+1\)
\(=3x^2-21xy-xy-3x-x+7y+y+7y^2+1\)
\(=\left(3x^2-21xy-3x\right)-\left(xy-7y^2-y\right)-\left(x-7y-1\right)\)
\(=3x\left(x-7y-1\right)-y\left(x-7y-1\right)-\left(x-7y-1\right)\)
\(=\left(x-7y-1\right)\left(3x-y-1\right)\)