
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a, Vì D là trung điểm BC => OD vuông BC
AM là tiếp tuyến với M là tiếp điểm nên ^AMO = 900
Xét tứ giác AMOD ta có
^AMO + ^ADO = 1800
mà 2 góc này đối
Vậy tứ giác AMOD nt 1 đường tròn
b, Xét tam giác AMB và tam giác ACM ta có
^AMB = ^ACM ( cùng chắn cung MB )
^A _ chung
Vậy tam giác AMB ~ tam giác ACM (g.g)
=> AM/AC = AB/AM => AM^2 = AB.AC
c, bạn ktra lại đề

b: Xét ΔAHC vuông tại H có HK là đường cao ứng với cạnh huyền AC
nên \(AH^2=AC\cdot AK\)
\(\Leftrightarrow\dfrac{AC}{2}=\dfrac{AH^2}{2\cdot AK}\)
hay \(HI=\dfrac{AH^2}{2\cdot AK}\)

bạn đăng tách ra nhé
1, Lấy vế cộng vế ta được \(\dfrac{4}{x-2}=4\Rightarrow x-2=1\Leftrightarrow x=3\)
Thay vào ta được \(\dfrac{2}{3-2}-\dfrac{3}{y+1}=1\Rightarrow\dfrac{3}{y+1}=1\Rightarrow y+1=3\Leftrightarrow y=2\)

Bài 8:
\(1,P=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ P=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\\ 2,P=2\Leftrightarrow2\sqrt{x}+4=3\sqrt{x}\Leftrightarrow\sqrt{x}=4\\ \Leftrightarrow x=16\left(tm\right)\)
Bài 9:
\(a,M=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ M=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\left(\sqrt{x}-1\right)\\ M=\dfrac{x-1}{\sqrt{x}}\\ b,M>0\Leftrightarrow x-1>0\left(\sqrt{x}>0\right)\\ \Leftrightarrow x>1\)
Bài 10:
\(a,A=\dfrac{\sqrt{\left(x+3\right)^2}}{x+3}=\dfrac{\left|x+3\right|}{x+3}\)
Với \(x\ge-3\Leftrightarrow A=\dfrac{x+3}{x+3}=1\)
Với \(x< -3\Leftrightarrow A=\dfrac{-\left(x+3\right)}{x+3}=-1\)
\(b,B=\dfrac{2}{x-1}\cdot\dfrac{\left|x-1\right|}{2\left|x\right|}\)
Với \(0< x< 1\Leftrightarrow B=\dfrac{2}{x-1}\cdot\dfrac{-\left(x-1\right)}{2x}=-\dfrac{1}{x}\)

Câu 2:
a:
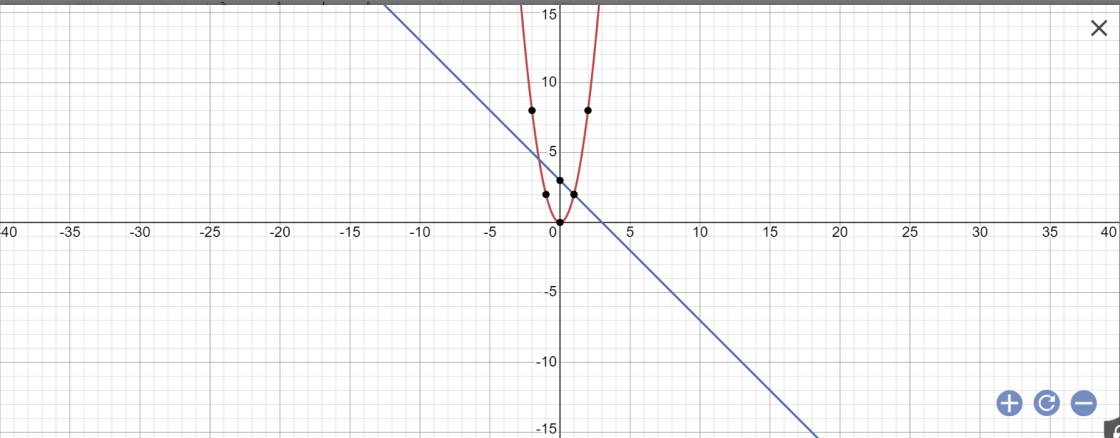
b: phương trình hoành độ giao điểm là:
\(2x^2=-x+3\)
=>\(2x^2+x-3=0\)
=>\(2x^2+3x-2x-3=0\)
=>(2x+3)(x-1)=0
=>\(\left[{}\begin{matrix}2x+3=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=1\end{matrix}\right.\)
Thay x=-3/2 vào (P), ta được:
\(y=2\cdot\left(-\dfrac{3}{2}\right)^2=2\cdot\dfrac{9}{4}=\dfrac{9}{2}\)
Thay x=1 vào (P), ta được:
\(y=2\cdot1^2=2\)
Vậy: (P) cắt (d) tại hai điểm là \(A\left(-\dfrac{3}{2};\dfrac{9}{2}\right);B\left(1;2\right)\)
 ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn
ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn 


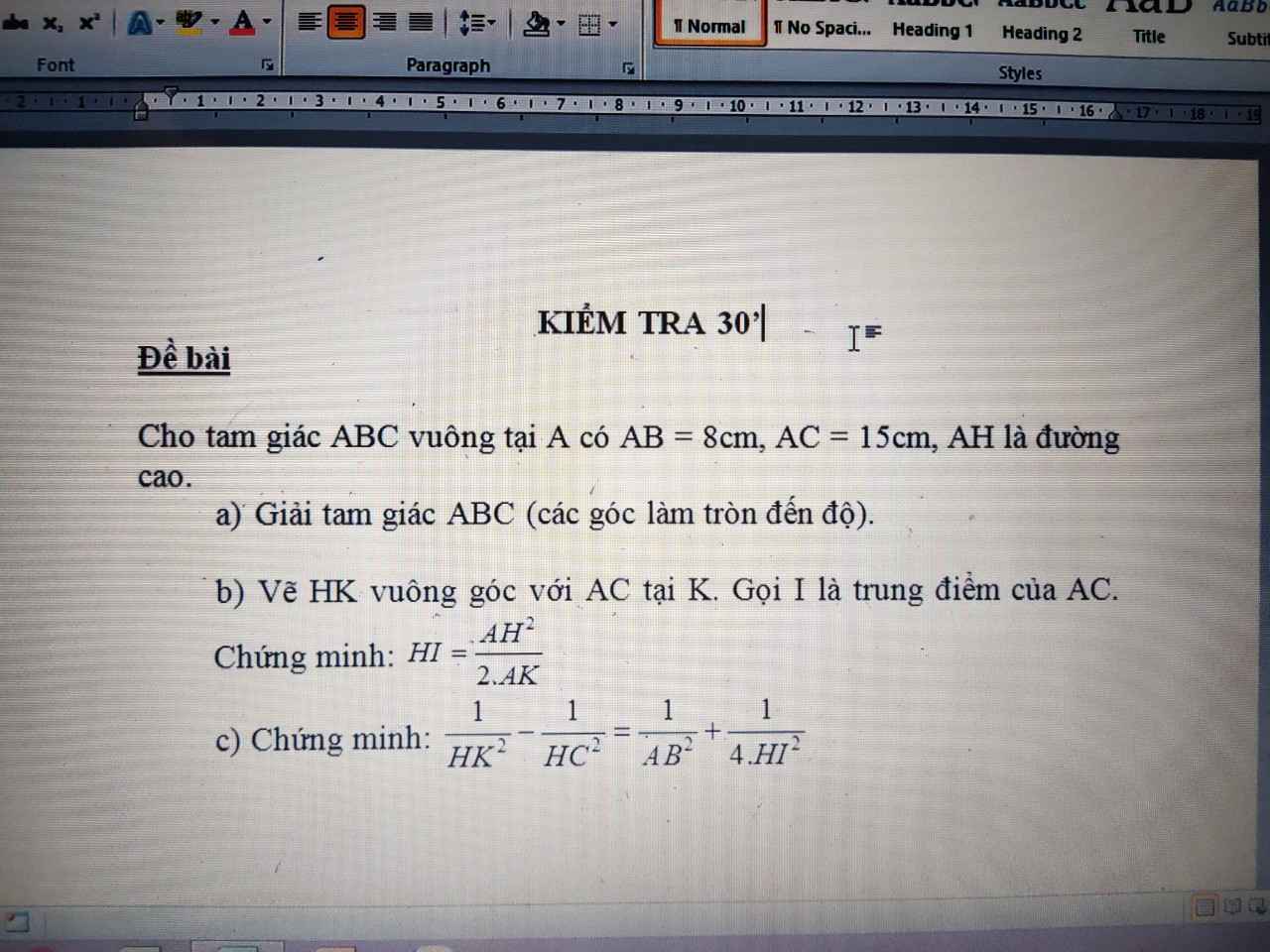

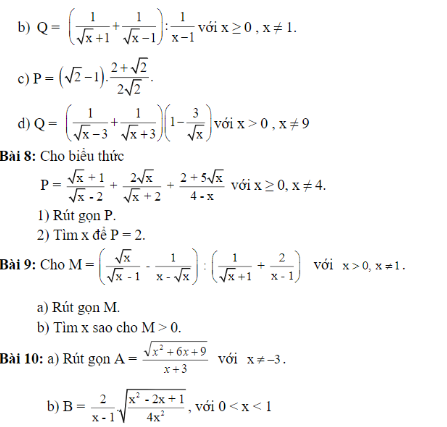

12.
a)
\(P=\dfrac{\sqrt{x}-1+1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}}{\left(\sqrt{x}-1\right)^2}\left(x>0;x\ne1\right)\\ P=\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}}=\dfrac{1}{\sqrt{x}}\)